Ada Apa Dengan Angka Penting?
Pengalaman Belajar fisika di SMAN BI 1 Banjar
(Sekolah Bertaraf Internasional)
SIGNIFICANT DIGITS
The number of significant digits in an answer to a calculation will depend on the number of significant digits in the given data, as discussed in the rules below.
Approximate calculations (order-of-magnitude estimates) always result in answers with only one or two significant digits.
When are Digits Significant?
Non-zero digits are always significant. Thus, 22 has two significant digits, and 22.3 has three significant digits.
With zeroes, the situation is more complicated: Zeroes placed before other digits are not significant; 0.046 has two significant digits.
Zeroes placed between other digits are always significant; 4009 kg has four significant digits. Zeroes placed after other digits but behind a decimal point are significant; 7.90 has three significant digits.
Zeroes at the end of a number are significant only if they are behind a decimal point as in (c).
Otherwise, it is impossible to tell if they are significant. For example, in the number 8200, it is not clear if the zeroes are significant or not. The number of significant digits in 8200 is at least two, but could be three or four. To avoid uncertainty, use scientific notation to place significant zeroes behind a decimal point:
8.2 ´ 103 has two significant digits
In a calculation involving multiplication, division, trigonometric functions, etc., the number of significant digits in an answer should equal the least number of significant digits in any one of the numbers being multiplied, divided etc.
Thus in evaluating sin(kx), where k = 0.097 m-1 (two significant digits) and x = 4.73 m (three significant digits), the answer should have two significant digits.
Note that whole numbers have essentially an unlimited number of significant digits. As an example, if a hair dryer uses 1.2 kW of power, then 2 identical hairdryers use 2.4 kW:
1.2 kW {2 sig. dig.} ´ 2 {unlimited sig. dig.} = 2.4 kW {2 sig. dig.}
Significant Digits in Addition and Subtraction
When quantities are being added or subtracted, the number of decimal places (not significant digits) in the answer should be the same as the least number of decimal places in any of the numbers being added or subtracted.
Example:
5.67 J (two decimal places)
1.1 J (one decimal place)
0.9378 J (four decimal place)
7.7 J (one decimal place)
Keep One Extra Digit in Intermediate Answers
When doing multi-step calculations, keep at least one more significant digit in intermediate results than needed in your final answer.
For instance, if a final answer requires two significant digits, then carry at least three significant digits in calculations. If you round-off all your intermediate answers to only two digits, you are discarding the information contained in the third digit, and as a result the second digit in your final answer might be incorrect.
(This phenomenon is known as "round-off error.")
(This phenomenon is known as "round-off error.")
The Two Greatest Sins Regarding Significant Digits
- Writing more digits in an answer (intermediate or final) than justified by the number of digits in the data.
- Rounding-off, say, to two digits in an intermediate answer, and then writing three digits in the final answer.
Identifying significant digits
The rules for identifying significant digits when writing or interpreting numbers are as follows:
- All non-zero digits are considered significant. For example, 91 has two significant figures (9 and 1), while 123.45 has five significant figures (1, 2, 3, 4 and 5).
- Zeros appearing anywhere between two non-zero digits are significant. Example: 101.12 has five significant figures: 1, 0, 1, 1 and 2.
- Leading zeros are not significant. For example, 0.00052 has two significant figures: 5 and 2.
- Trailing zeros in a number containing a decimal point are significant. For example, 12.2300 has six significant figures: 1, 2, 2, 3, 0 and 0. The number 0.000122300 still has only six significant figures (the zeros before the 1 are not significant). In addition, 120.00 has five significant figures. This convention clarifies the precision of such numbers; for example, if a result accurate to four decimal places is given as 12.23 then it might be understood that only two decimal places of accuracy are available. Stating the result as 12.2300 makes clear that it is accurate to four decimal places.
- The significance of trailing zeros in a number not containing a decimal point can be ambiguous. For example, it may not always be clear if a number like 1300 is accurate to the nearest unit (and just happens coincidentally to be an exact multiple of a hundred) or if it is only shown to the nearest hundred due to rounding or uncertainty. Various conventions exist to address this issue:
- A bar may be placed over the last significant digit; any trailing zeros following this are insignificant. For example,
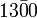 has three significant figures (and hence indicates that the number is accurate to the nearest ten).
has three significant figures (and hence indicates that the number is accurate to the nearest ten).
- A bar may be placed over the last significant digit; any trailing zeros following this are insignificant. For example,
- The last significant figure of a number may be underlined; for example, "20000" has two significant figures.
- A decimal point may be placed after the number; for example "100." indicates specifically that three significant figures are meant.
However, these conventions are not universally used, and it is often necessary to determine from context whether such trailing zeros are intended to be significant. If all else fails, the level of rounding can be specified explicitly.
The abbreviation s.f. is sometimes used, for example "20 000 to 2 s.f." or "20 000 (2 sf)". Alternatively, the uncertainty can be stated separately and explicitly, as in 20 000 ± 1%, so that significant-figures rules do not apply.
The abbreviation s.f. is sometimes used, for example "20 000 to 2 s.f." or "20 000 (2 sf)". Alternatively, the uncertainty can be stated separately and explicitly, as in 20 000 ± 1%, so that significant-figures rules do not apply.
Generally, the same rules apply to numbers expressed in scientific notation. However, in the normalized form of that notation, placeholder leading and trailing digits do not occur, so all digits are significant. For example, 0.00012 (two significant figures) becomes 1.2×10−4, and 0.000122300 (six significant figures) becomes 1.22300×10−4. In particular, the potential ambiguity about the significance of trailing zeros is eliminated. For example, 1300 to four significant figures is written as 1.300×103, while 1300 to two significant figures is written as 1.3×103.
Engineering notation
See main article on Engineering notation
Rounding
To round to n significant figures:
- Start with the leftmost non-zero digit (e.g. the "1" in 1200, or the "2" in 0.0256).
- Keep n digits. Replace the rest with zeros.
- Round up by one if appropriate. For example, if rounding 0.039 to 1 significant figure, the result would be 0.04. There are several different rules for handling borderline cases — seerounding for more details.
- Officially[2] if the first not significant figure is a 5 not followed by any other digits or followed only by zeros, the last significant figure should be rounded down or up to the nearest even number. So to round 1.25 to 2 significant figures should be 1.2 and 1.35 should be 1.4. If the first non-significant digit is a 5 followed by other non-zero digits, the last significant digit should be rounded up. For example, 1.2459 as the result of a calculation or measurement that only allows for 3 significant figures should be written 1.25.
Arithmetic
Main article: Significance arithmetic
For multiplication and division, the result should have as many significant figures as the measured number with the smallest number of significant figures.
For addition and subtraction, the result should have as many decimal places as the measured number with the smallest number of decimal places.
Importance
Superfluous precision
If a sprinter is measured to have completed a 100-metre race in 11.71 seconds, what is the sprinter's average speed? By dividing the distance by the time using a calculator, we get a speed of 8.53970965 m/s.
The most straightforward way to indicate the precision of this result (or any result) is to state the uncertainty separately and explicitly, for example in the above case as 8.5397±0.0037 m/s or equivalently 8.5397(37) m/s.
This is particularly appropriate when the uncertainty itself is important and precisely known (here, 100 m is presumed to be precise, and the time is 11.71±0.005 s, or an uncertainty of nearly 430 ppm).
In this case, it is safe and indeed advantageous to provide more digits than would be called for by the significant-figures rules.
This is particularly appropriate when the uncertainty itself is important and precisely known (here, 100 m is presumed to be precise, and the time is 11.71±0.005 s, or an uncertainty of nearly 430 ppm).
In this case, it is safe and indeed advantageous to provide more digits than would be called for by the significant-figures rules.
If the degree of precision in the answer is not important, it is again safe to express trailing digits that are not known exactly, for example 8.5397 m/s.
If, however, we are forced to apply significant-figures rules, expressing the result as 8.53970965 m/s would seem to imply that the speed is known to the nearest 10 nm/s or thereabouts, which would improperly overstate the precision of the measurement.
Reporting the result using three significant figures (8.54 m/s) might be interpreted as implying that the speed is somewhere between 8.535 and 8.545 m/s.
This is actually very close to the true precision, the actual speed being somewhere between 8.5360 and 8.5434 m/s.
Reporting the result using two significant figures (8.5 m/s) would introduce considerable roundoff error and degrade the precision of the result.
Reporting the result using three significant figures (8.54 m/s) might be interpreted as implying that the speed is somewhere between 8.535 and 8.545 m/s.
This is actually very close to the true precision, the actual speed being somewhere between 8.5360 and 8.5434 m/s.
Reporting the result using two significant figures (8.5 m/s) would introduce considerable roundoff error and degrade the precision of the result.
(Note: in actual practice, 100 m is not this precise!
For example, a pair of 0.05-metre-wide (2-inch) lines at the start and end would introduce a separate uncertainty of ±0.05 m (2 in) or 500 ppm to the above calculation.
Now the total uncertainty has risen to 500 + 430 = 930 ppm, since both sources must be added together.
Applied to the speed, that now becomes 8.5397±0.0080 or 8.5397(80) m/s, the actual speed being somewhere between 8.5317 and 8.5477 m/s.)
For example, a pair of 0.05-metre-wide (2-inch) lines at the start and end would introduce a separate uncertainty of ±0.05 m (2 in) or 500 ppm to the above calculation.
Now the total uncertainty has risen to 500 + 430 = 930 ppm, since both sources must be added together.
Applied to the speed, that now becomes 8.5397±0.0080 or 8.5397(80) m/s, the actual speed being somewhere between 8.5317 and 8.5477 m/s.)
Sumber:
Wikipedia























