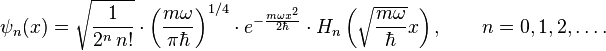Friday, 8 March 2013

Fisika Quantum: Ilusi atau Realita?

"I like relativity and quantum theories
Because I don’t understand them
And they make me feel as if space shifted
About like a swan that can’t settle
Refusing to sit still and be measured
And as if the atom were an impulsive thing
Always changing its mind."
~D. H. Lawrence~


PEOPLERESEARCHPUBLICATIONSEVENTS

Topik Penelitian Pada Pusat IPTEK Quantum di National University of Singapore 

Quantum mechanics (QM – also known as quantum physics quantum theory is a branch of physics dealing with physical phenomena at microscopic scales, where the action is on the order of the Planck constant. Quantum mechanics departs from classical mechanics primarily at the quantum realm of atomic and subatomic length scales. Quantum mechanics provides a mathematical description of much of the dual and behavior and interactions of energy and matter. 
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as infinite-dimensional Hilbert spaces and operators on these spaces.
Many of these structures are drawn from functional analysis, a research area within pure mathematics that was influenced in part by the needs of quantum mechanics. In brief, values of physical observables such as energy and momentum were no longer considered as values of functions on phase space, but as eigenvalues; more precisely: as spectral values (point spectrum plus absolute continuous plus singular continuous spectrum) of linear operators in Hilbert space.

Mathematical structure of quantum mechanics
A physical system is generally described by three basic ingredients: states; observables; and dynamics (or law of time evolution) or, more generally, a group of physical symmetries. A classical description can be given in a fairly direct way by a phase space model of mechanics: states are points in a symplectic phase space, observables are real-valued functions on it, time evolution is given by a one-parameter group of symplectic transformations of the phase space, and physical symmetries are realized by symplectic transformations.
A quantum description consists of a Hilbert space of states, observables are self adjoint operators on the space of states, time evolution is given by a one-parameter group of unitary transformations on the Hilbert space of states, and physical symmetries are realized by unitary transformations.

 Quantum harmonic oscillator
As in the classical case, the potential for the quantum harmonic oscillator is given by:
V(x)=\frac{1}{2}m\omega^2x^2
This problem can be solved either by solving the Schrödinger equation directly, which is not trivial, or by using the more elegant "ladder method", first proposed by Paul Dirac. Theeigenstates are given by:
\psi_n(x) = \sqrt{\frac{1}{2^n\,n!}} \cdot \left(\frac{m\omega}{\pi \hbar}\right)^{1/4} \cdot e^{ - \frac{m\omega x^2}{2 \hbar}} \cdot H_n\left(\sqrt{\frac{m\omega}{\hbar}} x \right), \qquad n = 0,1,2,\ldots.
where Hn are the Hermite polynomials:
H_n(x)=(-1)^n e^{x^2}\frac{d^n}{dx^n}\left(e^{-x^2}\right)
and the corresponding energy levels are
E_n = \hbar \omega \left(n + {1\over 2}\right).
This is another example which illustrates the quantization of energy for bound states.

Some Application of Quantum Mecahnics
Book Editor By: 
Prof. Mohammad Reza Pahlavani, Ph.D. 
Mazandaran University of Iran, Iran.

National University of Singapore Center for Quantum Technologies Graduate Student Theses


2012

2011

2010

2009

2008

Center for Quantum Technologies Software Projects

SOMIM

Search for Optimal Measurements using Iterative Methods (SOMIM), a program that can calculate the maximum mutual information and the corresponding optimal POVM outcomes given a set of statistical operators.

SeCQC

SeCQC is an open-source program code which implements a numerical Search for the classical Capacity of Quantum Channels (SeCQC) by using an iterative method. Given a quantum channel, SeCQC finds the statistical operators and POVM outcomes that maximize the accessible information, and thus determines the classical capacity of the quantum channel.

QCrypto

This is the repository for the source code used in a series of quantum key distribution experiments from key generation in form time-stamped detector data to error correction and privacy amplification. The code was designed to work with entanglement-based pair detection schemes, either implementing a BB84-type/BBM92 protocol, or an Ekert-91 protocol, which we used for our implementations of quantum key ditribution systems.


 Sources:

http://en.wikipedia.org/wiki/Quantum_mechanics

Center for Quantum Technologies

Arip Nurahman Notes

 Ucapan Terima Kasih:

1. Bpk. Dr. Miftachul Hadi, M.Sc. [Penulis dan Peneliti Fisika Produktif dari LIPI]

2. Kang Agus Haeruman, S.Si. [MTU Singapore]


Dan kepada teman-teman di Group Physics Research Consulting

Maju terus ilmu pengetahuan Indonesia, Semangat Kita Bisa

Amin.



Diposting oleh Astrophysics Boy di 05:00:00 0 komentar

Label: ,

Subscribe to: Posts (Atom)