~Soong to Data, in Star Trek~
Roket merupakan salah satu wahana dirgantara yang memiliki makna
strategis. Wahana ini mampu digunakan untuk melaksanakan misi perdamaian
maupun pertahanan, misalnya sebagai:
Roket Peluncur Satelit (RPS),
Roket penelitian cuaca,
Roket kendali,
Roket balistik dari : darat ke darat, darat ke udara dan udara ke udara.
Oleh sebab itu diperlukan upaya yang terus menerus untuk mewujudkan
kemandirian ini, salah satunya melalui usaha menumbuh kembangkan rasa
cinta teknologi dirgantara, khususnya teknologi peroketan sejak dini.
Dengan kata lain, roket juga bisa berfungsi sebagai peralatan untuk
menjaga kedaulatan dan meningkatkan martabat bangsa, baik di darat, laut
maupun di udara sampai dengan antariksa.
Oleh karena itu, negara yang menguasai kemandirian teknologi peroketan
dengan baik, akan disegani oleh negara-negara lain di seluruh dunia.
Indonesia sebagai negara besar dan luas sudah sepatutnya dapat meraih
kemandirian yang berkelanjutan dalam penguasaan teknologi roket.
Types of Rocket
› Science and Technology Website
› Strategic Technology Directions
› Research Topics
› Collaborations
› Opportunities
The Tsiolkovsky rocket equation, or ideal rocket equation, describes the motion of vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself (a thrust) by expelling part of its mass with high speed and move due to the conservation of momentum. The equation relates the delta-v (the maximum change of speed of the rocket if no other external forces act) with the effective exhaust velocity and the initial and final mass of a rocket (or other reaction engine).
 is the initial total mass, including propellant,
is the initial total mass, including propellant,
 is the final total mass,
is the final total mass,
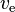 is the effective exhaust velocity (
is the effective exhaust velocity ( where
where 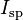 is the specific impulse expressed as a time period and
is the specific impulse expressed as a time period and 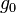 is Standard Gravity),
is Standard Gravity),
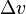 is delta-v - the maximum change of speed of the vehicle (with no external forces acting),
is delta-v - the maximum change of speed of the vehicle (with no external forces acting),
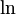 refers to the natural logarithm function.
refers to the natural logarithm function.
The equation is named after Konstantin Tsiolkovsky who independently derived it and published it in his 1903 work.
The Physics of Rocket
The Physics of Rocket
Derivation
Consider the following system:
In the following derivation, "the rocket" is taken to mean "the rocket and all of its unburned propellant".
Newton's second law of motion relates external forces (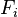 ) to the change in linear momentum of the system as follows:
) to the change in linear momentum of the system as follows:
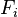 ) to the change in linear momentum of the system as follows:
) to the change in linear momentum of the system as follows:where
 is the momentum of the rocket at time t = 0:
is the momentum of the rocket at time t = 0:and
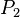 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time 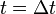 :
:and where, with respect to the observer:
 is the velocity of the rocket at time t = 0
is the velocity of the rocket at time t = 0
 is the velocity of the rocket at time
is the velocity of the rocket at time 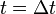
 is the velocity of the mass added to the exhaust (and lost by the rocket) during time
is the velocity of the mass added to the exhaust (and lost by the rocket) during time 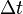
 is the mass of the rocket at time t = 0
is the mass of the rocket at time t = 0 is the mass of the rocket at time
is the mass of the rocket at time 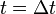
The velocity of the exhaust
 in the observer frame is related to the velocity of the exhaust in the rocket frame
in the observer frame is related to the velocity of the exhaust in the rocket frame  by (since exhaust velocity is in the negative direction)
by (since exhaust velocity is in the negative direction)Solving yields:
and, using
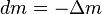 , since ejecting a positive
, since ejecting a positive 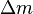 results in a decrease in mass,
results in a decrease in mass,If there are no external forces then
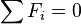 and
andAssuming
 is constant, this may be integrated to yield:
is constant, this may be integrated to yield:or equivalently
 or
or  or
or 
where
 is the initial total mass including propellant,
is the initial total mass including propellant,  the final total mass, and
the final total mass, and  the velocity of the rocket exhaust with respect to the rocket (the specific impulse, or, if measured in time, that multiplied by gravity-on-Earth acceleration).
the velocity of the rocket exhaust with respect to the rocket (the specific impulse, or, if measured in time, that multiplied by gravity-on-Earth acceleration).The value
 is the total mass of propellant expended, and hence:
is the total mass of propellant expended, and hence:where
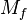 is the propellant mass fraction (the part of the initial total mass that is spent as reaction mass).
is the propellant mass fraction (the part of the initial total mass that is spent as reaction mass). (delta v)
is the integration over time of the magnitude of the acceleration
produced by using the rocket engine (what would be the actual
acceleration if external forces were absent). In free space, for the
case of acceleration in the direction of the velocity, this is the
increase of the speed. In the case of an acceleration in opposite
direction (deceleration) it is the decrease of the speed.
(delta v)
is the integration over time of the magnitude of the acceleration
produced by using the rocket engine (what would be the actual
acceleration if external forces were absent). In free space, for the
case of acceleration in the direction of the velocity, this is the
increase of the speed. In the case of an acceleration in opposite
direction (deceleration) it is the decrease of the speed.Of course gravity and drag also accelerate the vehicle, and they can add or subtract to the change in velocity experienced by the vehicle. Hence delta-v is not usually the actual change in speed or velocity of the vehicle.
If special relativity is taken into account, the following equation can be derived for a relativistic rocket, with
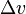 again standing for the rocket's final velocity (after burning off all its fuel and being reduced to a rest mass of
again standing for the rocket's final velocity (after burning off all its fuel and being reduced to a rest mass of  ) in the inertial frame of reference where the rocket started at rest (with the rest mass including fuel being
) in the inertial frame of reference where the rocket started at rest (with the rest mass including fuel being  initially), and
initially), and  standing for the speed of light in a vacuum:
standing for the speed of light in a vacuum:Writing
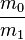 as
as  , a little algebra allows this equation to be rearranged as
, a little algebra allows this equation to be rearranged asThen, using the identity
![R^{\frac{2v_e}{c}} = \exp \left[ \frac{2v_e}{c} \ln R \right]](http://upload.wikimedia.org/math/e/3/b/e3b8f025908827a823dbef5fb35ce629.png) (here "exp" denotes the exponential function;
(here "exp" denotes the exponential function; see also Natural logarithm as well as the "power" identity at Logarithm#Logarithmic identities) and the identity
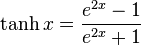 (see Hyperbolic function), this is equivalent to
(see Hyperbolic function), this is equivalent toApplicability
Pendidikan, Riset dan Kompetisi Pembuatan Iptek Roket di Tanah Air
Uses
The rocket equation captures the essentials of rocket flight physics in a single short equation. It also holds true for rocket-like reaction vehicles whenever the effective exhaust velocity is constant; and can be summed or integrated when the effective exhaust velocity varies. It does not apply to non-rocket systems, such as aerobraking, gun launches, space elevators, launch loops, tether propulsion.
The rocket equation captures the essentials of rocket flight physics in a single short equation. It also holds true for rocket-like reaction vehicles whenever the effective exhaust velocity is constant; and can be summed or integrated when the effective exhaust velocity varies. It does not apply to non-rocket systems, such as aerobraking, gun launches, space elevators, launch loops, tether propulsion.
Delta-v is of fundamental importance in orbital mechanics. It quantifies how difficult it is to perform a given orbital maneuver. To achieve a large delta-v, either  must be huge (growing exponentially as delta-v rises), or
must be huge (growing exponentially as delta-v rises), or  must be tiny, or
must be tiny, or 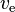 must be very high, or some combination of all of these.
must be very high, or some combination of all of these.
 must be huge (growing exponentially as delta-v rises), or
must be huge (growing exponentially as delta-v rises), or  must be tiny, or
must be tiny, or 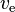 must be very high, or some combination of all of these.
must be very high, or some combination of all of these.
In practice, very-high delta-v has been achieved by a combination of 1) very large rockets (increasing  ), 2) staging (decreasing
), 2) staging (decreasing  ), and 3) very high exhaust velocities.
), and 3) very high exhaust velocities.
 ), 2) staging (decreasing
), 2) staging (decreasing  ), and 3) very high exhaust velocities.
), and 3) very high exhaust velocities.The Saturn V rocket used in the Apollo space program is an example of a large, serially staged rocket. The Space Shuttle is an example of parallel staging where all of its engines are ignited on the ground and some (the solid rocket boosters) are jettisoned to lose weight before reaching orbit.
The ion thruster
is an example of a high exhaust velocity rocket. Instead of storing
energy in the propellant itself as in a chemical rocket, ion and other
electric rockets separate energy storage from the reaction (propellant)
mass storage.
Not only does this allow very large (and in principle unlimited) amounts of energy to be applied to small amounts of ejected mass to achieve very high exhaust velocities, but energy sources far more compact than chemical fuels can be used, such as nuclear reactors. In the inner solar system solar power can be used, entirely eliminating the need for a large internal primary energy storage system.
Not only does this allow very large (and in principle unlimited) amounts of energy to be applied to small amounts of ejected mass to achieve very high exhaust velocities, but energy sources far more compact than chemical fuels can be used, such as nuclear reactors. In the inner solar system solar power can be used, entirely eliminating the need for a large internal primary energy storage system.
Sources:
1. Tsiolkovsky Rocket Equation
2. NASA Jet Propulsion Laboratory
3. Lembaga Penerbangan dan Antariksa Nasional (LAPAN)
Arungilah luasnya jagat raya cosmos
Rengkuhlah mimpi-mimpi hingga bintang-gemintang
Bukalah tabir rahasia-rahasia langit
Temukan Ke-Maha'an Sang Pencipta
Kunjungi juga sekolah Online Kami dalam Bidang Ilmu Pengetahuan Ke Luar Angkasa'an
Indonesian Space Sciences & Technology School
Sebuah persembahan sederhana dari para ilmuwan muda tanah air untuk kemajuan peradaban umat manusia.
Indonesian University Space Research Association

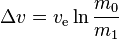
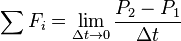




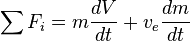



![\frac{m_0}{m_1} = \left[\frac{1 + {\frac{\Delta v}{c}}}{1 - {\frac{\Delta v}{c}}}\right]^{\frac{c}{2v_e}}](http://upload.wikimedia.org/math/5/3/6/5364f100e69e5406e28a8740039d6070.png)



























