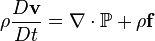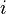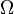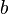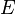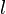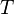Tahun 2008 telah datang dengan serangkaian Event Astronomi yang cukup menarik. Saatnya untuk menandai Kalender Astronomi kita saat terjadi event yang cukup menarik untuk kita saksikan. Di bawah ini telah kami susun Kalender Astronomi yang berlaku di indonesia selama tahun 2008 ini. Kalender astronomi ini meliputi fase bulan, meteor shower, gerhana, okultasi, oposisi, konjungsi serta beberapa event yang lain. Beberapa event tersebut dapat disaksikan hanya menggunakan mata telanjang atau mungkin perlu binokuler atau bahkan harus menggunakan teleskop.
.
Kalender Event Astronomi Indonesia ini disusun berdasarkan beberapa sumber yaitu Efemeris NASA, Program Planetarium Starrynight dan Generator SkyViewCafe juga mengambil dari beberapa sumber diantaranya U.S. Naval Observatory dan NASA/Goddard Space Flight Center. Kita berharap akan mendapatkan langit cerah saat melakukan observasi walaupun langit di negeri kita selalu banyak bertabur awan. Happy stargazing, Clear & Dark Sky.
.
8 Januari 2008 @ 18:38 WIB GS - Bulan Baru, Awal Muharram 1429 H
..
4 Januari 2008 @ 03:00 WIB - Quadrantids Meteor Shower. Pagi hari di langit Timur kita dapat saksikan beberapa goresan meteor ini sampai sebelum langit benderang. Prediski 60 meteor per jam untuk tahun ini.
.
22 Januari 2008 @ 20:36 WIB GS - Bulan Purnama..
22 Januari 2008 @ 11:47 WIB GS - Mercury Greatest Eastern Elongation. Planet Merkurius pada posisi Elongasi Maksimum di sebelah Timur Matahari. Hari ini ini jarak sudut elongasi Merkurius terhadap matahari mencapai maksimum hampir sekitar 19°. Saat paling bagus menyaksikan planet ini di Langit Barat sore hari sesudah matahari terbenam.
.
1 Februari 2008 @ 04:00 WIB - Jupiter - Venus Conjunction. Hari ini Planet Jupiter dan Planet Venus mengalami konjungsi yaitu berada pada jarak yang sangat dekat. Kedua planet hanya terpisah pada jarak 0,6° saat pagi hari di Langit Timur.
.
7 Februari 2008 @ 10:46 WIB GS - Bulan Baru, Awal Shafar 1429 H
.
7 Februari 2008 @ 10:55 WIB GS - Annular Solar Eclipse. Hari ini terjadi Gerhana Matahari Cincin (GMC). Proses gerhana maksimum hanya dapat diamati daerah Antartika. Sedangkan daerah yang dapat melihat proses Gerhana Sebagian meliputi New Zealand sebagian daerah Selatan Australia. Gerhana tidak dapat diamati dari Indonesia. ( Informasi & Animasi )
.
11 Februari 2008 @ 08:53 WIB GS - Neptune Conjunction. Posisi Planet Neptunus tepat di belakang Matahari.
.
21 Februari 2008 @ 10:30 WIB GS - Bulan Purnama
. .
21 Februari 2008 @ 10:26 WIB GS - Total Lunar Eclipse. Hari ini terjadi Gerhana Bulan Total (GBT). Proses keseluruhan gerhana hanya dapat disaksikan di daratan Amerika, Afrika, dan Eropa. Indonesia tidak berpeluang mengamati peristiwa ini. ( Informasi )
.
24 Februari 2008 @ 16:29 WIB GS - Saturn at Opposition. Oposisi Planet Saturnus. Planet bercincin Saturnus berada pada fase Purnama dan berada paling dekat dengan Bumi. Saat terbaik untuk melakukan pengamatan dan pengambilan foto planet ini bersama beberapa bulannya.
.
3 Maret 2008 @ 14:19 WIB GS - Mercury Greatest Western Elongation. Planet Merkurius pada posisi Elongasi Maksimum di sebelah Barat Matahari. Hari ini ini jarak sudut elongasi Merkurius terhadap matahari mencapai maksimum hampir sekitar 19°. Saat paling bagus menyaksikan planet ini di Langit Timur sore hari sebelum matahari terbit.
..
7 Maret 2008 @ 00:16 WIB GS - Bulan Baru, Awal Rabiul Awal 1429 H
.
9 Maret 2008 @ 03:08 WIB GS - Uranus at Conjunction. Posisi Planet Uranus tepat di belakang Matahari.
.
20 Maret 2008 @ 12:48 WIB GS - Vernal Equinox. Hari ini panjang siang sama dengan malam hari. Vernal Equinox adalah saat matahari melintas (berada tepat) di ekuator dan masuk di zona belahan Bumi Utara. Di Indonesia event ini menandai awal Musim Kemarau, sedangkan di Belahan Bumi Utara menandai awal Musim Semi (Spring). Sementara di Belahan Bumi Selatan menandai awal Musim Gugur (Autum/Fall).
...
21 Maret 2008 @ 01:40 WIB GS - Bulan Purnama
.
6 April 2008 @ 10:55 WIB GS - Bulan Baru, Awal Rabiul Akhir 1429 H
.
16 April 2008 @ 14:17 WIB GS - Mercury at Superior Conjunction. Posisi Planet Merkurius berada tepat di belakang Matahari.
.
20 April 2008 @ 17:26 WIB GS - Bulan Purnama
.
22 April 2008 @ 02:00 WIB - Lyrids Meteor Shower. Shower ini dapat dilihat mulai lepas tengah malam hingga pagi hari di belahan Langit Timur.. Prediksi 10 meteor per jam atau lebih mungkin bisa nampak.
.
5 Mei 2008 @ 19:20 WIB GS - Bulan Baru, Awal Jumadil Awal 1429 H
.
5 Mei 2008 @ 02:00 WIB - Eta Aquarids Meteor Shower. Shower ini dapat disaksikan mulai lepas tengah malam hingga menjelang pagi hari di belahan Langit Timur. Prediksi 30 meteor atau lebih setiap jam mungkin dapat disaksikan.
.
14 Mei 2008 @ 10:51 WIB GS - Mercury Greatest Estern Elongation. Planet Merkurius pada posisi Elongasi Maksimum di sebelah Timur Matahari. Hari ini ini jarak sudut elongasi Merkurius terhadap matahari mencapai maksimum hampir sekitar 19°. Saat paling bagus menyaksikan planet ini di Langit Barat sore hari sesudah matahari terbenam.
.
20 Mei 2008 @ 09:12 WIB GS - Bulan Purnama
.
3 Juni 2008 @ 02:24 WIB GS - Bulan Baru, Awal Jumadil Akhir 1429 H
..
7 Juni 2008 @ 22:29 WIB GS - Mercury Inferior Conjunction. Posisi Planet Merkurius berada tepat di depan Matahari, posisinya diantara Bumi dan Matahari.
.
9 Juni 2008 @ 10:51 WIB GS - Venus Superior Conjunction. Posisi Planet Venus berada tepat di belakang Matahari.
.
18 Juni 2008 @ 00:30 WIB GS - Bulan Purnama
.
21 Juni 2008 @ 06:59 WIB GS - Summer Solstice. Adalah saat matahari berada di titik paling Utara atau sering disebut sebagai Tropic of Cancer yaitu garis paralel 23º 27’ di Utara ekuator Bumi. Hari ini siang paling panjang di Belahan Utara dan paling pendek di Selatan. Dan perhatikan serta amati, terbit/terbenamnya matahari akan mulai bergeser lagi ke Selatan.
.. .
21 Juni 2008 @ 02:13 WIB GS - Pluto Opposition. Hari ini Planet Pluto pada fase purnama, tepat di atas kita saat tengah malam.
2 Juli 2008 @ 10:25 WIB GS - Mercury Greatest Western Elongation. Planet Merkurius pada posisi Elongasi Maksimum di sebelah Barat Matahari. Hari ini ini jarak sudut elongasi Merkurius terhadap matahari mencapai maksimum hampir sekitar 19°. Saat paling bagus menyaksikan planet ini di Langit Timur sore hari sebelum matahari terbit.
.
3 Juli 2008 @ 09:20 WIB - Bulan Baru, Awal Rajab 1429 H
.
9 Juli 2008 @ 14:20 WIB GS - Jupiter Opposition. Planet Jupiter berada pada fase Purnama atau beroposisi. Hari ini planet raksasa ini berada pada jarak terdekatnya dengan Bumi. Saat terbaik untuk melakukan pengamatan dan pengambilan foto Planet Jupiter ini bersama 4 bulannya bulannya yang terkenal itu.
..
18 Juli 2008 @ 15:00 WIB GS - Bulan Purnama
.
27 Juli 2008 @ 21:00 WIB - Southern Delta Aquarids Meteor Shower. Meteor shower ini dapat diamati mulai pukul 21:00 hingga menjelang pagi. Arah radiant mulai dari Timur saat sore dan bergerak ke Barat hingga pagi harinya. Prediksi 10-20 meteor mungkin bisa disaksikan.
.
30 Juli 2008 @ 02:57 WIB GS - Mercury Superior Conjunction. Posisi Planet Merkurius berada tepat di belakang Matahari.
.
1 Agustus 2008 @ 17:14 WIB GS - Bulan Baru, Awal Syaban 1429 H
.
1 Agustus 2008 @ 17:21 WIB GS - Total Solar Eclipse. Gerhana Matahari Total (GMT) terjadi pada hari ini. Jalur gerhana total mulai dari Kanada Utara lalu bergerak melintasi Greenland, Siberia, Mongolia dan China. Sedangkan beberapa lokasi yang dapat melihat gerhana sebagian adalah Greenland, Eropa dan Asia Barat. Sedangkan dari Indonesia tidak dapat diamati. ( Informasi & Animasi )
.
12 Agustus 2008 @ 01:00 WIB - Perseids Meteor Shower. Meteor shower ini dapat disaksikan di belahan Langit Timur mulai lepas tengah malam dinihari hingga pagi hari sebelum terang. Prediksi 50-80 meteor setiap jam mungkin dapat disaksikan pada kondisi langit yang bagus.
.
15 Agustus 2008 @ 14:21 WIB GS - Neptune at Opposition. Planet Neptunus berada pada fase purnama atau sedang beroposisi. Si planet Biru ini berada pada jarak yang paling dekat dengan Bumi. Sekarang adalah saat paling bagus untuk mengamati planet ini, namun ia hanya akan nampak sebagai titik cahaya berwarna biru walau menggunakan teleskop yang kuat.
.16 Agustus 2008 @ 04:10 WIB - Partial Lunar Eclipse. Hari ini terjadi Gerhana Bulan Sebagian (GBS). Gerhana dapat diamati mulai dari Amerika Selatan, Eropa, Afrika, Asia, dan Australia. Sedangkan dari Indonesia gerhana ini dapat disaksikan mulai pukul 03:30 pagi di Langit Barat bisa diamati sampai sebelum bulan tenggelam. ( Informasi )
17 Agustus 2008 @ 04:16 WIB GS - Bulan Purnama
.

.
31 Agustus 2008 @ 03:00 WIB GS - Bulan Baru, "Awal Ramadhan 1429 H"
.
4 September 2008 @ 08:48 WIB GS - Saturn Conjunction. Posisi Planet Saturnus kali ini berada tepat di belakang Matahari.
.
11 September 2008 @ 06:52 WIB GS - Mercury Greatest Eastern Elongation. Planet Merkurius pada posisi Elongasi Maksimum di sebelah Timur Matahari. Hari ini ini jarak sudut elongasi Merkurius terhadap matahari mencapai maksimum hampir sekitar 19°. Saat paling bagus menyaksikan planet ini di Langit Barat sore hari sesudah matahari terbenam.
.
13 September 2008 @ 08:55 WIB GS - Uranus at Opposition. Planet Neptunus berada pada fase purnama atau sedang beroposisi. Planet berwarna kehijauan ini berada pada jarak paling dekatnya dengan Bumi. Sekarang adalah saat paling bagus untuk mengamati Uranus, namun ia hanya akan nampak sebagai titik cahaya berwarna biru kehijauan walau menggunakan teleskop yang kuat.
..
15 September 2008 @ 16:14 WIB GS - Bulan Purnama
.
22 September 2008 @ 22:44 WIB GS - Autumnal Equinox. Adalah saat dimana posisi matahari tepat berada di garis ekuator melanjutkan gerak semu hariannya ke arah Selatan. Equinox terjadi dua kali selama setahun yaitu Maret Equinox dan September Equinox. Pada September Equinox matahari akan melanjutkan gerak semu hariannya ke arah Selatan. Hari ini panjang siang tepat sama dengan malam, tidak ada bayangan di katulistiwa saat tengah hari. Awal Musim Gugur (Autum/Falling) di belahan bumi Utara dan Awal Musim Semi (Spring) di belahan bumi Selatan.
..
29 September 2008 @ 15:14 WIB GS - Bulan Baru, "Awal Syawwal 1429 H" .
.
7 Oktober 2008 @ 03:50 WIB GS - Mercury Inferior Conjunction. Posisi Planet Merkurius berada tepat di depan Matahari, posisinya diantara Bumi dan Matahari.
.
14 Oktober 2008 @ 03:02 WIB GS - Bulan Purnama
.
21 Oktober 2008 @ 01:00 WIB - Orionids Meteor Shower. Dapat disaksikan lepas tengah malam di belahan Langit Timur hingga pagi. Prediksi 40 meteor setiap jam mungkin bisa berkurang akibat kemunculan bulan malam itu.
.
22 Oktober 2008 @ 12:32 WIB GS - Mercury Greatest Western Elongation. Planet Merkurius pada posisi Elongasi Maksimum di sebelah Barat Matahari. Hari ini ini jarak sudut elongasi Merkurius terhadap matahari mencapai maksimum hampir sekitar 19°. Saat paling bagus menyaksikan planet ini di Langit Timur sore hari sebelum matahari terbit.
.
29 Oktober 2008 @ 06:16 WIB GS - Bulan Baru, Awal Zulqaidah 1429 H
.
13 November 2008 @ 13:19 WIB GS - Bulan Purnama
.
19 November 2008 @ 23:00 WIB - Leonids Meteor Shower. Meteor Shower ini dapat diamati menjelang tengah malam sampai sebelum fajar. Radiant meteor ini berada di arah Timur-Laut tepatnya di kepala Rasi Leo. Rasi ini tampak di langit Timur lepas pukul 02:00 dinihari. Leonids dapat menampakkan sekitar 10 sampai 15 meteor setiap jam saat puncaknya. Kali ini pengamatan Leonids tidak maksimal karena terganggu oleh cahaya bulan.
..
25 November 2008 @ 23:37 WIB GS - Mercury Superior Conjunction. Posisi Planet Merkurius berada tepat di belakang Matahari.
.
27 November 2008 @ 23:56 WIB GS - Bulan Baru, "Awal Zulhijjah 1429 H"
..
1 Desember 2008 @ 19:30 WIB - Moon-Venus-Jupiter Conjunction . Bulan sabit, Planet Venus dan Planet Jupiter dalam formasi segitiga pada jarak hanya sekitar 3° antara ketiganya. Pemandangan ini dapat disaksikan pada sore hari selepas Isya'.
.
6 Desember 2008 @ 04:28 WIB - Mars Conjunction. Posisi Planet Merkurius berada tepat di belakang Matahari.
.
12 Desember 2008 @ 23:38 WIB GS - Bulan Purnama
..
14 Desember 2008 @ 21:00 WIB - Geminids Meteor Shower. Shower ini dapat disaksikan mulai pukul 21:00 sampai menjelang pagi. Radiant meteor ini berada di arah Timur-Laut tepatnya di Rasi Gemini. Rasi ini tampak di langit Timur mulai pukul 20:00 WIB waktu sore dan terus bergerak ke Barat hingga pagi. Geminids dapat menampakkan sampai 120 meteor setiap jam saat puncaknya. Waktu terbaik untuk pengamatan adalah setelah radiant muncul sekitar pukul 21:00 WIB saat bulan sudah terbenam hingga pagi hari sebelum cahaya Timur merembang. Kali ini pengamatan Geminids tidak akan bisa maksimal disebabkan terganggu oleh cahaya bulan purnama.
. .
21 Desember 2008 @ 19:04 WIB GS - Winter Solstice. Adalah saat matahari berada di titik paling Selatan atau sering disebut sebagai Tropic of Capricorn yaitu garis paralel 23º 27’ di Selatan ekuator Bumi. Hari ini siang paling pendek di Belahan Utara dan paling panjang di Selatan. Dan perhatikan serta amati, terbit/terbenamnya matahari akan mulai bergeser lagi ke Utara.
.
22 Desember 2008 @ 16:18 WIB GS - Pluto Conjunction Posisi Planet Pluto berada tepat di belakang Matahari.
.
27 Desember 2008 @ 19:24 WIB GS - Bulan Baru, Awal Muharram 1430 H
Sumber: Terimakasih kepada Bapak Mutoha yang telah mengijinkan tulisannya disadur di web blog Banjar Astrophysics Association (Jogja Astro Club)

Solar eclipse
A solar eclipse occurs when the Moon passes between the Sun and the Earth so that the Sun is wholly or partially obscured. This can only happen during a new moon, when the Sun and Moon are in conjunction as seen from the Earth. At least two and up to five solar eclipses occur each year on Earth, with between zero and two of them being total eclipses.[citation needed] Total solar eclipses are nevertheless rare at any location because during each eclipse totality exists only along a narrow corridor in the relatively tiny area of the Moon's umbra.
A total solar eclipse is a spectacular natural phenomenon and many people travel to remote locations to observe one. The 1999 total eclipse in Europe helped to increase public awareness of the phenomenon, as illustrated by the number of journeys made specifically to witness the 2005 annular eclipse and the 2006 total eclipse. The most recent solar eclipse occurred on August 1, 2008, and was a total eclipse.
In ancient times, and in some cultures today, solar eclipses have been attributed to supernatural causes. Total solar eclipses can be frightening for people who are unaware of their astronomical explanation, as the Sun seems to disappear in the middle of the day and the sky darkens in a matter of minutes.
Contents
Types
There are four types of solar eclipses:
- A total eclipse occurs when the Sun is completely obscured by the Moon. The intensely bright disk of the Sun is replaced by the dark silhouette of the Moon, and the much fainter corona is visible. During any one eclipse, totality is visible only from at most a narrow track on the surface of the Earth.
- An annular eclipse occurs when the Sun and Moon are exactly in line, but the apparent size of the Moon is smaller than that of the Sun. Hence the Sun appears as a very bright ring, or annulus, surrounding the outline of the Moon.
- A hybrid eclipse is intermediate between a total and annular eclipse. At some points on the surface of the Earth it is visible as a total eclipse, whereas at others it is annular. Hybrid eclipses are rather rare.
- A partial eclipse occurs when the Sun and Moon are not exactly in line, and the Moon only partially obscures the Sun. This phenomenon can usually be seen from a large part of the Earth outside of the track of an annular or total eclipse. However, some eclipses can only be seen as a partial eclipse, because the umbra never intersects the Earth's surface.
The match between the apparent sizes of the Sun and Moon during a total eclipse is a coincidence. The Sun's distance from the Earth is about 400 times the Moon's distance, and the Sun's diameter is about 400 times the Moon's diameter. Because these ratios are approximately the same, the sizes of the Sun and the Moon as seen from Earth appear to be approximately the same: about 0.5 degree of arc in angular measure.
Because the Moon's orbit around the Earth is an ellipse, as is the Earth's orbit around the Sun, the apparent sizes of the Sun and Moon vary.[1][2] The magnitude of an eclipse is the ratio of the apparent size of the Moon to the apparent size of the Sun during an eclipse. An eclipse when the Moon is near its closest distance from the Earth (i.e., near its perigee) can be a total eclipse because the Moon will appear to be large enough to cover completely the Sun's bright disk, or photosphere; a total eclipse has a magnitude greater than 1. Conversely, an eclipse when the Moon is near its farthest distance from the Earth (i.e., near its apogee) can only be an annular eclipse because the Moon will appear to be slightly smaller than the Sun; the magnitude of an annular eclipse is less than 1. Slightly more solar eclipses are annular than total because, on average, the Moon lies too far from Earth to cover the Sun completely. A hybrid eclipse occurs when the magnitude of an eclipse is very close to 1: the eclipse will appear to be total at some locations on Earth and annular at other locations.[3]
The Earth's orbit around the Sun is also elliptical, so the Earth's distance from the Sun varies throughout the year. This also affects the apparent sizes of the Sun and Moon, but not so much as the Moon's varying distance from the Earth. When the Earth approaches its farthest distance from the Sun (the aphelion) in July, this tends to favor a total eclipse. As the Earth approaches its closest distance from the Sun (the perihelion) in January, this tends to favor an annular eclipse.
Terminology
Central eclipse is often used as a generic term for a total, annular, or hybrid eclipse. This is, however, not completely correct: the definition of a central eclipse is an eclipse during which the central line of the umbra touches the Earth's surface. It is possible, though extremely rare, that part of the umbra intersects with Earth (thus creating an annular or total eclipse), but not its central line. This is then called a non-central total or annular eclipse.[5]
The term solar eclipse itself is strictly speaking a misnomer. The phenomenon of the Moon passing in front of the Sun is not an eclipse, but an occultation. Properly speaking, an eclipse occurs when one object passes into the shadow cast by another object. For example, when the Moon disappears at full moon by passing into Earth's shadow, the event is properly called a lunar eclipse. Therefore, technically, a solar eclipse actually amounts to an eclipse of the Earth.
 Lunar Eclipse
Lunar EclipseA
lunar eclipse occurs whenever the Moon passes through some portion of the Earth's shadow. This can occur only when the
Sun,
Earth, and
Moon are aligned exactly, or very closely so, with the Earth in the middle. Hence, there is always a
full moon the night of a lunar eclipse. The type and length of an eclipse depend upon the Moon's location relative to its
orbital nodes. The
next total lunar eclipse occurs on December 21, 2010.
Contents
Types of lunar eclipses
The shadow of the Earth can be divided into two distinctive parts: the umbra and penumbra. Within the umbra, there is no direct solar radiation. However, as a result of the Sun's large angular size, solar illumination is only partially blocked in the outer portion of the Earth's shadow, which is given the name penumbra.
A penumbral eclipse occurs when the Moon passes through the Earth's penumbra. The penumbra does not cause any noticeable darkening of the Moon's surface, though some may argue it turns a little yellow. A special type of penumbral eclipse is a total penumbral eclipse, during which the Moon lies exclusively within the Earth's penumbra. Total penumbral eclipses are rare, and when these occur, that portion of the Moon which is closest to the umbra can appear somewhat darker than the rest of the Moon.
A partial lunar eclipse occurs when only a portion of the Moon enters the umbra. When the Moon travels completely into the Earth's umbra, one observes a total lunar eclipse. The Moon's speed through the shadow is about one kilometer per second (2,300 mph), and totality may last up to nearly 107 minutes. Nevertheless, the total time between the Moon's first and last contact with the shadow is much longer, and could last up to 3.8 hours.[1] The relative distance of the Moon from the Earth at the time of an eclipse can affect the eclipse's duration. In particular, when the Moon is near its apogee, the farthest point from the Earth in its orbit, its orbital speed is the slowest. The diameter of the umbra does not decrease much with distance. Thus, a totally-eclipsed Moon occurring near apogee will lengthen the duration of totality.
A selenelion or selenehelion occurs when both the Sun and the eclipsed Moon can be observed at the same time. This can only happen just before sunset or just after sunrise, and both bodies will appear just above the horizon at nearly opposite points in the sky. This arrangement has led to the phenomenon being referred to as a horizontal eclipse. It happens during every lunar eclipse at all those places on the Earth where it is sunrise or sunset at the time. Indeed, the reddened light that reaches the Moon comes from all the simultaneous sunrises and sunsets on the Earth. Although the Moon is in the Earth's geometrical shadow, the Sun and the eclipsed Moon can appear in the sky at the same time because the refraction of light through the Earth's atmosphere causes objects near the horizon to appear higher in the sky than their true geometric position.[2]
The Moon does not completely disappear as it passes through the umbra because of the refraction of sunlight by the Earth's atmosphere into the shadow cone; if the Earth had no atmosphere, the Moon would be completely dark during an eclipse. The red colouring arises because sunlight reaching the Moon must pass through a long and dense layer of the Earth's atmosphere, where it is scattered. Shorter wavelengths are more likely to be scattered by the small particles, and so by the time the light has passed through the atmosphere, the longer wavelengths dominate. This resulting light we perceive as red. This is the same effect that causes sunsets and sunrises to turn the sky a reddish colour; an alternative way of considering the problem is to realise that, as viewed from the Moon, the Sun would appear to be setting (or rising) behind the Earth.
The amount of refracted light depends on the amount of dust or clouds in the atmosphere; this also controls how much light is scattered. In general, the dustier the atmosphere, the more that other wavelengths of light will be removed (compared to red light), leaving the resulting light a deeper red colour. This causes the resulting coppery-red hue of the Moon to vary from one eclipse to the next. Volcanoes are notable for expelling large quantities of dust into the atmosphere, and a large eruption shortly before an eclipse can have a large effect on the resulting colour.
Danjon scale
The following scale (the Danjon scale) was devised by André Danjon for rating the overall darkness of lunar eclipses:[3]
- L=0: Very dark eclipse. Moon almost invisible, especially at mid-totality.
- L=1: Dark Eclipse, gray or brownish in colouration. Details distinguishable only with difficulty.
- L=2: Deep red or rust-colored eclipse. Very dark central shadow, while outer edge of umbra is relatively bright.
- L=3: Brick-red eclipse. Umbral shadow usually has a bright or yellow rim.
- L=4: Very bright copper-red or orange eclipse. Umbral shadow is bluish and has a very bright rim.
Eclipse cycles
- See also: Saros cycle and Eclipse cycle
Every year there are usually at least two partial lunar eclipses, although total eclipses are significantly less common. If one knows the date and time of an eclipse, it is possible to predict the occurrence of other eclipses using an eclipse cycle like the Saros cycle. Unlike a solar eclipse, which can only be viewed from a certain relatively small area of the world, a lunar eclipse may be viewed from anywhere on the night side of the Earth.
Further Sources:
Wikipedia


 is the fluid density,
is the fluid density, is the substantive derivative (also called the material derivative),
is the substantive derivative (also called the material derivative), is the velocity vector,
is the velocity vector,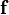 is the body force vector, and
is the body force vector, and is a tensor that represents the surface forces applied on a fluid particle (the comoving stress tensor).
is a tensor that represents the surface forces applied on a fluid particle (the comoving stress tensor). is a symmetric tensor. In general, (in three dimensions)
is a symmetric tensor. In general, (in three dimensions)  has the form:
has the form: are normal stresses, and
are normal stresses, and are tangential stresses (shear stresses).
are tangential stresses (shear stresses). is the velocity gradient perpendicular to the direction of shear
is the velocity gradient perpendicular to the direction of shear