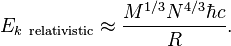How the Sun Shines
by John N. Bahcall
29 June2000
Edited and add By:
Arip Nurahman
Department of Physics, Faculty of sciences and Mathematics
Indonesia University of Education
What makes the sun shine? How does the sun produce the vast amount of energy necessary to support life on earth? These questions challenged scientists for a hundred and fifty years, beginning in the middle of the nineteenth century. Theoretical physicists battled geologists and evolutionary biologists in a heated controversy over who had the correct answer.
Why was there so much fuss about this scientific puzzle? The nineteenth-century astronomer John Herschel described eloquently the fundamental role of sunshine in all of human life in his 1833 Treatise on Astronomy:
The sun's rays are the ultimate source of almost every motion which takes place on the surface of the earth. By its heat are produced all winds,...By their vivifying action vegetables are elaborated from inorganic matter, and become, in their turn, the support of animals and of man, and the sources of those great deposits of dynamical efficiency which are laid up for human use in our coal strata.
Sunshine makes life possible on earth.
In this essay, we shall review from an historical perspective the development of our understanding of how the sun (the nearest star) shines, beginning in the following section with the nineteenth-century controversy over the age of the sun. In later sections, we shall see how seemingly unrelated discoveries in fundamental physics led to a theory of nuclear energy generation in stars that resolved the controversy over the age of the sun and explained the origin of solar radiation. In the section just before the summary, we shall discuss how experiments that were designed to test the theory of nuclear energy generation in stars revealed a new mystery, the Mystery of the Missing Neutrinos.
The Age of the Sun
How old is the sun? How does the sun shine? These questions are two sides of the same coin, as we shall see.
The rate at which the sun is radiating energy is easily computed by using the measured rate at which energy reaches the earth's surface and the distance between the earth and the sun. The total energy that the sun has radiated away over its lifetime is approximately the product of the current rate at which energy is being emitted, which is called the solar luminosity, times the age of the sun.
The older the sun is, the greater the total amount of radiated solar energy. The greater the radiated energy, or the larger the age of the sun, the more difficult it is to find an explanation of the source of solar energy.
To better appreciate how difficult it is to find an explanation, let us consider a specific illustration of the enormous rate at which the sun radiates energy. Suppose we put a cubic centimeter of ice outside on a summer day in such a way that all of the sunshine is absorbed by the ice. Even at the great distance between the earth and the sun, sunshine will melt the ice cube in about 40 minutes. Since this would happen anywhere in space at the earth's distance from the sun, a huge spherical shell of ice centered on the sun and 300 million km (200 million miles) in diameter would be melted at the same time. Or, shrinking the same amount of ice down to the surface of the sun, we can calculate that an area ten thousand times the area of the earth's surface and about half a kilometer (0.3 mile) thick would also be melted in 40 minutes by the energy pouring out of the sun.
In this section, we shall discuss how nineteenth-century scientists tried to determine the source of solar energy, using the solar age as a clue.
Conflicting Estimates of the Solar Age
The energy source for solar radiation was believed by nineteenth-century physicists to be gravitation. In an influential lecture in 1854, Hermann von Helmholtz, a German professor of physiology who became a distinguished researcher and physics professor, proposed that the origin of the sun's enormous radiated energy is the gravitational contraction of a large mass. Somewhat earlier, in the 1840s, J.R. Mayer (another German physician) and J.J. Waterson had also suggested that the origin of solar radiation is the conversion of gravitational energy into heat.1
Biologists and geologists considered the effects of solar radiation, while physicists concentrated on the origin of the radiated energy. In 1859, Charles Darwin, in the first edition of On The Origin of the Species by Natural Selection, made a crude calculation of the age of the earth by estimating how long it would take erosion occurring at the current observed rate to wash away the Weald, a great valley that stretches between the North and South Downs across the south of England. He obtained a number for the "denudation of the Weald'' in the range of 300 million years, apparently long enough for natural selection to have produced the astounding range of species that exist on earth.
As Herschel stressed, the sun's heat is responsible for life and for most geological evolution on earth. Hence, Darwin's estimate of a minimum age for geological activity on the earth implied a minimum estimate for the amount of energy that the sun has radiated.
Firmly opposed to Darwinian natural selection, William Thompson, later Lord Kelvin, was a professor at the University of Glasgow and one of the great physicists of the nineteenth century. In addition to his many contributions to applied science and to engineering, Thompson formulated the second law of thermodynamics and set up the absolute temperature scale, which was subsequently named the Kelvin scale in his honor. The second law of thermodynamics states that heat naturally flows from a hotter to a colder body, not the opposite. Thompson therefore realized that the sun and the earth must get colder unless there is an external energy source and that eventually the earth will become too cold to support life.
Kelvin, like Helmholtz, was convinced that the sun's luminosity was produced by the conversion of gravitational energy into heat. In an early (1854) version of this idea, Kelvin suggested that the sun's heat might be produced continually by the impact of meteors falling onto its surface. Kelvin was forced by astronomical evidence to modify his hypothesis and he then argued that the primary source of the energy available to the sun was the gravitational energy of the primordial meteors from which it was formed.
Thus, with great authority and eloquence Lord Kelvin declared in 1862:
That some form of the meteoric theory is certainly the true and complete explanation of solar heat can scarcely be doubted, when the following reasons are considered: (1) No other natural explanation, except by chemical action, can be conceived. (2) The chemical theory is quite insufficient, because the most energetic chemical action we know, taking place between substances amounting to the whole sun's mass, would only generate about 3,000 years' heat. (3) There is no difficulty in accounting for 20,000,000 years' heat by the meteoric theory.
Kelvin continued by attacking Darwin's estimate directly, asking rhetorically:
What then are we to think of such geological estimates as [Darwin's] 300,000,000 years for the "denudation of the Weald''?
Believing Darwin was wrong in his estimate of the age of the earth, Kelvin also believed that Darwin was wrong about the time available for natural selection to operate.
Lord Kelvin estimated the lifetime of the sun, and by implication the earth, as follows. He calculated the gravitational energy of an object with a mass equal to the sun's mass and a radius equal to the sun's radius and divided the result by the rate at which the sun radiates away energy. This calculation yielded a lifetime of only 30 million years. The corresponding estimate for the lifetime sustainable by chemical energy was much smaller because chemical processes release very little energy.
Who Was Right?
As we have just seen, in the nineteenth century you could get very different estimates for the age of the sun, depending upon whom you asked. Prominent theoretical physicists argued, based upon the sources of energy that were known at that time, that the sun was at most a few tens of million years old. Many geologists and biologists concluded that the sun must have been shining for at least several hundreds of millions of years in order to account for geological changes and the evolution of living things, both of which depend critically upon energy from the sun. Thus the age of the sun, and the origin of solar energy, were important questions not only for physics and astronomy, but also for geology and biology.
Darwin was so shaken by the power of Kelvin's analysis and by the authority of his theoretical expertise that in the last editions of On The Origin of the Species he eliminated all mention of specific time scales. He wrote in 1869 to Alfred Russel Wallace, the codiscoverer of natural selection, complaining about Lord Kelvin:
Thompson's views on the recent age of the world have been for some time one of my sorest troubles.
Today we know that Lord Kelvin was wrong and the geologists and evolutionary biologists were right. Radioactive dating of meteorites shows that the sun is 4.6 billion years old.
What was wrong with Kelvin's analysis? An analogy may help. Suppose a friend observed you using your computer and tried to figure out how long the computer had been operating. A plausible estimate might be no more than a few hours, since that is the maximum length of time over which a battery could supply the required amount of power. The flaw in this analysis is the assumption that your computer is necessarily powered by a battery. The estimate of a few hours could be wrong if you computer were operated from an electrical power outlet in the wall. The assumption that a battery supplies the power for your computer is analogous to Lord Kelvin's assumption that gravitational energy powers the sun.
Since nineteenth century theoretical physicists did not know about the possibility of transforming nuclear mass into energy, they calculated a maximum age for the sun that was too short. Nevertheless, Kelvin and his colleagues made a lasting contribution to the sciences of astronomy, geology, and biology by insisting on the principle that valid inferences in all fields of research must be consistent with the fundamental laws of physics.
We will now discuss some of the landmark developments in the understanding of how nuclear mass is used as the fuel for stars.
A Glimpse of the Solution
The turning point in the battle between theoretical physicists and empirical geologists and biologists occurred in 1896. In the course of an experiment designed to study x-rays discovered the previous year by Wilhelm Röntgen, Henri Becquerel stored some uranium-covered plates in a desk drawer next to photographic plates wrapped in dark paper. Because it was cloudy in Paris for a couple of days, Becquerel was not able to "energize'' his photographic plates by exposing them to sunlight as he had intended. On developing the photographic plates, he found to his surprise strong images of his uranium crystals. He had discovered natural radioactivity, due to nuclear transformations of uranium.
The significance of Becquerel's discovery became apparent in 1903, when Pierre Curie and his young assistant, Albert Laborde, announced that radium salts constantly release heat. The most extraordinary aspect of this new discovery was that radium radiated heat without cooling down to the temperature of its surroundings. The radiation from radium revealed a previously unknown source of energy. William Wilson and George Darwin almost immediately proposed that radioactivity might be the source of the sun's radiated energy.
The young prince of experimental physics, Ernest Rutherford, then a professor of physics at McGill University in Montreal, discovered the enormous energy released by alpha particle radiation from radioactive substances. In 1904, he announced:
The discovery of the radio-active elements, which in their disintegration liberate enormous amounts of energy, thus increases the possible limit of the duration of life on this planet, and allows the time claimed by the geologist and biologist for the process of evolution.
The discovery of radioactivity opened up the possibility that nuclear energy might be the origin of solar radiation. This development freed theorists from relying in their calculations on gravitational energy. However, subsequent astronomical observations showed that the sun does not contain a lot of radioactive materials, but instead is mostly hydrogen in gaseous form. Moreover, the rate at which radioactivity delivers energy does not depend on the stellar temperature, while observations of stars suggested that the amount of energy radiated by a star does depend sensitively upon the star's interior temperature. Something other than radioactivity is required to release nuclear energy within a star.
In the next sections, we shall trace the steps that led to what we now believe is the correct understanding of how stars shine.
The Direction Established
The next fundamental advance came once again from an unexpected direction. In 1905, Albert Einstein derived his famous relation between mass and energy, E = mc2, as a consequence of the special theory of relativity. Einstein's equation showed that a tiny amount of mass could, in principle, be converted into a tremendous amount of energy. His relation generalized and extended the nineteenth century law of conservation of energy of von Helmholtz and Mayer to include the conversion of mass into energy.
What was the connection between Einstein's equation and the energy source of the sun? The answer was not obvious. Astronomers did their part by defining the constraints that observations of stars imposed on possible explanations of stellar energy generation. In 1919, Henry Norris Russell, the leading theoretical astronomer in the United States, summarized in a concise form the astronomical hints on the nature of the stellar energy source. Russell stressed that the most important clue was the high temperature in the interiors of stars.
Aston showed in 1920 that four hydrogen nuclei are heavier than a helium nucleus.
F.W. Aston discovered in 1920 the key experimental element in the puzzle. He made precise measurements of the masses of many different atoms, among them hydrogen and helium. Aston found that four hydrogen nuclei were heavier than a helium nucleus. This was not the principal goal of the experiments he performed, which were motivated in large part by looking for isotopes of neon.
The importance of Aston's measurements was immediately recognized by Sir Arthur Eddington, the brilliant English astrophysicist. Eddington argued in his 1920 presidential address to the British Association for the Advancement of Science that Aston's measurement of the mass difference between hydrogen and helium meant that the sun could shine by converting hydrogen atoms to helium. This burning of hydrogen into helium would (according to Einstein's relation between mass and energy) release about 0.7% of the mass equivalent of the energy. In principle, this could allow the sun to shine for about a 100 billion years.
In a frighteningly prescient insight, Eddington went on to remark about the connection between stellar energy generation and the future of humanity:
If, indeed, the sub-atomic energy in the stars is being freely used to maintain their great furnaces, it seems to bring a little nearer to fulfillment our dream of controlling this latent power for the well-being of the human race---or for its suicide.
Understanding the Process
The next major step in understanding how stars produce energy from nuclear burning, resulted from applying quantum mechanics to the explanation of nuclear radioactivity. This application was made without any reference to what happens in stars. According to classical physics, two particles with the same sign of electrical charge will repel each other, as if they were repulsed by a mutual recognition of 'bad breath'. Classically, the probability that two positively charged particles get very close together is zero. But, some things that cannot happen in classical physics can occur in the real world which is described on a microscopic scale by quantum mechanics.
In 1928, George Gamow, the great Russian-American theoretical physicist, derived a quantum-mechanical formula that gave a non-zero probability of two charged particles overcoming their mutual electrostatic repulsion and coming very close together. This quantum mechanical probability is now universally known as the "Gamow factor.'' It is widely used to explain the measured rates of certain radioactive decays.
In the decade that followed Gamow's epochal work, Atkinson and Houtermans and later Gamow and Teller used the Gamow factor to derive the rate at which nuclear reactions would proceed at the high temperatures believed to exist in the interiors of stars. The Gamow factor was needed in order to estimate how often two nuclei with the same sign of electrical charge would get close enough together to fuse and thereby generate energy according to Einstein's relation between excess mass and energy release.
In 1938, C.F. von Weizsäcker came close to solving the problem of how some stars shine. He discovered a nuclear cycle, now known as the carbon-nitrogen-oxygen (CNO) cycle, in which hydrogen nuclei could be burned using carbon as a catalyst. However, von Weizsäcker did not investigate the rate at which energy would be produced in a star by the CNO cycle nor did he study the crucial dependence upon stellar temperature.
The CNO Cycle
For stars heavier than the sun, theoretical models show that the CNO (carbon-nitrogen-oxygen) cycle of nuclear fusion is the dominant source of energy generation. The cycle results in the fusion of four hydrogen nuclei (1H, protons) into a single helium nucleus (4He, alpha particle), which supplies energy to the star in accordance with Einstein's equation. Ordinary carbon,12C, serves as a catalyst in this set of reactions and is regenerated. Only relatively low energy neutrinos ()are produced in this cycle.
The figure is adapted from J.N. Bahcall, Neutrinos from the Sun, Scientific American, Volume 221, Number 1, July 1969, pp. 28-37.
By April 1938, it was almost as if the scientific stage had been intentionally set for the entry of Hans Bethe, the acknowledged master of nuclear physics. Professor Bethe had just completed a classic set of three papers in which he reviewed and analyzed all that was then known about nuclear physics. These works were known among his colleagues as "Bethe's bible.'' Gamow assembled a small conference of physicists and astrophysicists in Washington, D.C. to discuss the state of knowledge, and the unsolved problems, concerning the internal constitution of the stars.
In the course of the next six months or so, Bethe worked out the basic nuclear processes by which hydrogen is burned (fused) into helium in stellar interiors. Hydrogen is the most abundant constituent of the sun and similar stars, and indeed the most abundant element in the universe.
Bethe described the results of his calculations in a paper entitled "Energy Production in Stars,'' which is awesome to read. He authoritatively analyzed the different possibilities for reactions that burn nuclei and selected as most important the two processes that we now believe are responsible for sunshine. One process, the so-called p-p chain, builds helium out of hydrogen and is the dominant energy source in stars like the sun and less massive stars.
The p—p Chain Reaction
In theoretical models of the sun, the p—p chain of nuclear reactions illustrated here is the dominant source of energy production. Each reaction is labeled by a number in the upper left hand corner of the box in which it is contained. In reaction 1, two hydrogen nuclei (1H, protons) are fused to produce a heavy hydrogen nucleus (2H, a deuteron). This is the usual way nuclear burning gets started in the sun. On rare occasions, the process is started by reaction 2. Deuterons produced in reactions 1 and 2 fuse with protons to produce a light element of helium (3He). At this point, the p—p chain breaks into three branches, whose relative frequencies are indicated in the figure. The net result of this chain is the fusion of four protons into a single ordinary helium nucleus (4He) with energy being released to the star in accordance with Einstein's equation. Particles called 'neutrinos' () are emitted in these fusion processes. Their energies are shown in the figure in units of millions of electron volts (MeV). Reactions 2 and 4 were not discussed by Hans Bethe.
The figure is adapted from J.N. Bahcall, Neutrinos from the Sun, Scientific American, Volume 221, Number 1, July 1969, pp. 28-37.
The CNO cycle, the second process which was also considered by von Weizsäcker, is most important in stars that are more massive than the sun. Bethe used his results to estimate the central temperature of the sun and obtained a value that is within 20% of what we currently believe is the correct value (16 million degrees Kelvin).2 Moreover, he showed that his calculations led to a relation between stellar mass and stellar luminosity that was in satisfactory agreement with the available astronomical observations.
In the first two decades after the end of the second world war, many important details were added to Bethe's theory of nuclear burning in stars. Distinguished physicists and astrophysicists, especially A.G.W. Cameron, W.A. Fowler, F. Hoyle, E.E. Salpeter, M. Schwarzschild, and their experimental colleagues, returned eagerly to the question of how stars like the sun generate energy. From Bethe's work, the answer was known in principle: the sun produces the energy it radiates by burning hydrogen. According to this theory, the solar interior is a sort of controlled thermonuclear bomb on a giant scale.3 The theory leads to the successful calculation of the observed luminosities of stars similar to the sun and provides the basis for our current understanding of how stars shine and evolve over time. The idea that nuclear fusion powers stars is one of the cornerstones of modern astronomy and is used routinely by scientists in interpreting observations of stars and galaxies.
W.A. Fowler, Willy as he was universally known, led a team of colleagues in his Caltech Kellogg Laboratory and inspired physicists throughout the world to measure or calculate the most important details of the p-p chain and the CNO cycle. There was plenty of work to do and the experiments and the calculations were difficult. But, the work got done because understanding the specifics of solar energy generation was so interesting. Most of the efforts of Fowler and his colleagues M. Burbidge, G.R. Burbidge, F. Hoyle, and A.G.W. Cameron) soon shifted to the problem of how the heavy elements, which are needed for life, are produced in stars.
Testing the Hypothesis of Nuclear Burning
Science progresses as a result of the clash between theory and experiment, between speculation and measurement. Eddington, in the same lecture in which he first discussed the burning of hydrogen nuclei in stars, remarked:
I suppose that the applied mathematician whose theory has just passed one still more stringent test by observation ought not to feel satisfaction, but rather disappointment --- "Foiled again! This time I had hoped to find a discordance which would throw light on the points where my model could be improved.''
Is there any way to test the theory that the sun shines because very deep in its interior hydrogen is burned into helium? At first thought, it would seem impossible to make a direct test of the nuclear burning hypothesis. Light takes about ten million years to leak out from the center of the sun to the surface and when it finally emerges in the outermost regions, light mainly tells us about the conditions in those outer regions. Nevertheless, there is a way of "seeing'' into the solar interior with neutrinos, exotic particles discovered while trying to understand a different mystery.4
Discovery, Confirmation, and Surprise
A neutrino is a sub-atomic particle that interacts weakly with matter and travels at a speed that is essentially the speed of light. Neutrinos are produced in stars when hydrogen nuclei are burned to helium nuclei; neutrinos are also produced on earth in particle accelerators, in nuclear reactors, and in natural radioactivity. Based upon the work of Hans Bethe and his colleagues, we believe that the process by which stars like the sun generate energy can be symbolized by the relation,
(1)
in which four hydrogen nuclei (1H, protons) are burned into a single helium nucleus (4He, particle) plus two positive electrons () and two neutrinos () plus energy. This process releases energy to the star since, as Aston showed, four hydrogen atoms are heavier than one helium atom. The same set of nuclear reactions that supply the energy of the sun's radiation also produce neutrinos that can be searched for in the laboratory.
This figure is a cross section of the sun. The features that are usually studied by astronomers with normal telescopes that detect light are labeled on the outside, e. g., sunspot and prominences. Neutrinos enable us to look deep inside the sun, into the solar core where nuclear burning occurs.
Because of their weak interactions, neutrinos are difficult to detect. How difficult? A solar neutrino passing through the entire earth has less than one chance in a thousand billion of being stopped by terrestrial matter. According to standard theory, about a hundred billion solar neutrinos pass through your thumbnail every second and you don't notice them. Neutrinos can travel unaffected through iron as far as light can travel in a hundred years through empty space.
In 1964, Raymond Davis Jr. and I proposed that an experiment with 100,000 gallons of cleaning fluid (perchloroethylene, which is mostly composed of chlorine) could provide a critical test of the idea that nuclear fusion reactions are the ultimate source of solar radiation. We argued that, if our understanding of nuclear processes in the interior of the sun was correct, then solar neutrinos would be captured at a rate Davis could measure with a large tank filled with cleaning fluid. When neutrinos interact with chlorine, they occasionally produce a radioactive isotope of argon. Davis had shown previously that he could extract tiny amounts of neutrino-produced argon from large quantities of perchloroethylene. To do the solar neutrino experiment, he had to be spectacularly clever since according to my calculations only, a few atoms would be produced per week in a huge Olympic-sized swimming pool of cleaning fluid.
Our sole motivation for urging this experiment was to use neutrinos to:
enable us to see into the interior of a star and thus verify directly the hypothesis of nuclear energy generation in stars.
As we shall see, Davis and I did not anticipate some of the most interesting aspects of this proposal.
Davis performed the experiment and in 1968 announced the first results. He measured fewer neutrinos than I predicted. As the experiment and the theory were refined, the disagreement appeared more robust. Scientists rejoiced that solar neutrinos were detected but worried why there were fewer neutrinos than predicted.
What was wrong? Was our understanding of how the sun shines incorrect? Had I made an error in calculating the rate at which solar neutrinos would be captured in Davis's tank? Was the experiment wrong? Or, did something happen to the neutrinos after they were created in the sun?
Over the next twenty years, many different possibilities were examined by hundreds, and perhaps thousands, of physicists, chemists, and astronomers5. Both the experiment and the theoretical calculation appeared to be correct.
Once again experiment rescued pure thought. In 1986, Japanese physicists led by Masatoshi Koshiba and Yoji Totsuka, together with their American colleagues, Eugene Beier and Alfred Mann, reinstrumented a huge tank of water designed to measure the stability of matter. The experimentalists increased the sensitivity of their detector so that it could also serve as a large underground observatory of solar neutrinos. Their goal was to explore the reason for the quantitative disagreement between the predicted and the measured rates in the chlorine experiment.
The new experiment (called Kamiokande) in the Japanese Alps also detected solar neutrinos. Moreover, the Kamiokande experiment confirmed that the neutrino rate was less than predicted by standard physics and standard models of the sun and demonstrated that the detected neutrinos came from the sun. Subsequently, experiments in Russia (called SAGE, led by V. Gavrin), in Italy (GALLEX and later GNO led by T. Kirsten and E. Belotti, respectively), and again in Japan (Super-Kamiokande, led by Y. Totsuka and Y. Suzuki), each with different characteristics, all observed neutrinos from the solar interior. In each detector, the number of neutrinos observed was somewhat lower than standard theory predicted.
What do all of these experimental results mean?
Neutrinos produced in the center of the sun have been detected in five experiments. Their detection shows directly that the source of the energy that the sun radiates is the fusion of hydrogen nuclei in the solar interior. The nineteenth century debate between theoretical physicists, geologists, and biologists has been settled empirically.
From an astrophysical perspective, the agreement between neutrino observations and theory is good. The observed energies of the solar neutrinos match the values predicted by theory. The rates at which neutrinos are detected are less than predicted but not by a large factor. The predicted neutrino arrival rate at the earth depends approximately upon the 25th power of the central temperature of the sun, T x T x...T (25 factors of the temperature T). The agreement that has been achieved (agreement within a factor of three) shows that we have empirically measured the central temperature of the sun to an accuracy of a few percent. Incidentally, if someone had told me in 1964 that the number of neutrinos observed from the sun would be within a factor of three of the predicted value, I would have been astonished and delighted.
In fact, the agreement between normal astronomical observations (using light rather than neutrinos) and theoretical calculations of solar characteristics is much more precise. Studies of the internal structure of the sun using the solar equivalent of terrestrial seismology (i. e., observations of solar vibrations) show that the predictions of the standard solar model for the temperatures in the central regions of the sun are consistent with the observations to an accuracy of at least 0.1%. In this standard model, the current age of the sun is five billion years, which is consistent with the minimum estimate of the sun's age made by nineteenth-century geologists and biologists (a few hundred million years).
Given that the theoretical models of the sun describe astronomical observations accurately, what can explain the disagreement by a factor of two or three between the measured and the predicted solar neutrino rates?
New Physics
Physicists and astronomers were once again forced to reexamine their theories. This time, the discrepancy was not between different estimates of the sun's age, but rather between predictions based upon a widely accepted theory and direct measurements of particles produced by nuclear burning in the sun's interior. This situation was sometimes referred to as the Mystery of the Missing Neutrinos or, in language that sounded more scientific, the Solar Neutrino Problem.
As early as 1969, two scientists working in Russia, Bruno Pontecorvo and Vladimir Gribov, proposed that the discrepancy between standard theory and the first solar neutrino experiment could be due to an inadequacy in the textbook description of particle physics, rather than in the standard solar model. (Incidentally, Pontecorvo was the first person to propose using a chlorine detector to study neutrinos.) Gribov and Pontecorvo suggested that neutrinos suffer from a multiple personality disorder, that they oscillate back and forth between different states or types.
According to the suggestion of Gribov and Pontecorvo, neutrinos are produced in the sun in a mixture of individual states, a sort of split personality. The individual states have different, small masses, rather than the zero masses attributed to them by standard particle theory. As they travel to the earth from the sun, neutrinos oscillate between the easier-to-detect neutrino state and the more difficult-to-detect neutrino state. The chlorine experiment only detects neutrinos in the easier-to-observe state. If many of the neutrinos arrive at earth in the state that is difficult to observe, then they are not counted. It is as if some or many of the neutrinos have vanished, which can explain the apparent mystery of the missing neutrinos.
Building upon this idea, Lincoln Wolfenstein in 1978 and Stanislav Mikheyev and Alexei Smirnov in 1985 showed that the effects of matter on neutrinos moving through the sun might increase the oscillation probability of the neutrinos if Nature has chosen to give them masses in a particular range.
Neutrinos are also produced by the collisions of cosmic ray particles with other particles in the earth's atmosphere. In 1998, the Super-Kamiokande team of experimentalists announced that they had observed oscillations among atmospheric neutrinos. This finding provided indirect support for the theoretical suggestion that solar neutrinos oscillate among different states. Many scientists working in the field of solar neutrinos believe that, in retrospect, we have had evidence for oscillations of solar neutrinos since 1968.
But, we do not yet know what causes the multiple personality disorder of solar neutrinos. The answer to this question may provide a clue to physics beyond the current standard models of sub-atomic particles. Does the change of identity occur while the neutrinos are traveling to the earth from the sun, as originally proposed by Gribov and Pontecorvo? Or does matter cause solar neutrinos to "flip out''? Experiments are underway in Canada, Italy (three experiments), Japan (two experiments), Russia, and the United States that are attempting to determine the cause of the oscillations of solar neutrinos, by finding out how much they weigh and how they transform from one type to another. Non-zero neutrino masses may provide a clue to a still undiscovered realm of physical theory.
Nature: A Wonderful Mystery
Nature has written a wonderful mystery. The plot continually changes and the most important clues come from seemingly unrelated investigations. These sudden and drastic changes of scientific scene appear to be Nature's way of revealing the unity of all fundamental science.
The mystery begins in the middle of the nineteenth century with the puzzle: How does the sun shine? Almost immediately, the plot switches to questions about how fast natural selection occurs and at what rate geological formations are created. The best theoretical physics of the nineteenth century gave the wrong answer to all these questions. The first hint of the correct answer came, at the very end of the nineteenth century, from the discovery of radioactivity with accidentally darkened photographic plates.
The right direction in which to search for the detailed solution was revealed by the 1905 discovery of the special theory of relativity, by the 1920 measurement of the nuclear masses of hydrogen and helium, and by the 1928 quantum mechanical explanation of how charged particles get close to each other. These crucial investigations were not directly related to the study of stars.
By the middle of the twentieth century, nuclear physicists and astrophysicists could calculate theoretically the rate of nuclear burning in the interiors of stars like the sun. But, just when we thought we had Nature figured out, experiments showed that fewer solar neutrinos were observed at earth than were predicted by the standard theory of how stars shine and how sub-atomic particles behave.
At the beginning of the twenty-first century, we have learned that solar neutrinos tell us not only about the interior of the sun, but also something about the nature of neutrinos. No one knows what surprises will be revealed by the new solar neutrino experiments that are currently underway or are planned. The richness and the humor with which Nature has written her mystery, in an international language that can be read by curious people of all nations, is beautiful, awesome, and humbling.
Bibliography
l. F.W. Aston, "The Mass-Spectra of Chemical Elements,'' Philosophical Magazine and Journal of Science, 39, 611-625 (1920). In the course of a systematic program to measure the masses of atoms, Aston found that four hydrogen nuclei (protons) are heavier than a helium nucleus (an alpha particle) and two positive electrons [see Eq. (1)]. This fundamental discovery is the experimental basis of our understanding of how stars like the sun shine. The original paper is rarely cited, perhaps because the text is mainly devoted to a description of Aston's new apparatus and to a discussion of the many different masses that he measured. The hydrogen-helium mass difference is only briefly discussed.
2. R.D.E. Atkinson and F.G. Houtermans, "Zur Frage der Aufbaumöglichkeit der Elements in Sternen,''
Z. Physik 54, 656 (1929). An early attempt to calculate the rate of nuclear reactions in stars using the Gamow factor.
3. J.N. Bahcall, "Solar Neutrinos I. Theoretical,'' Phys. Rev. Lett. 12, 300 (1964).
4. H.A. Bethe, "Energy production in Stars,'' Phys. Rev. 55, 436 (1939). If you are a physicist and only have time to read one paper in the subject, this is the paper to read.
5. J.D. Burchfield, Lord Kelvin and The Age of the Earth, (Chicago: University of Chicago Press), 1990. This concise book provides a clear and insightful account of Kelvin's views on the age of the earth and the age of the sun, and on many other topics including natural selection and geological evolution. The author tells an exciting story with historical accuracy.
6. C.L. Cowan Jr., F. Reines, F.B. Harrison, H.W. Kruse, and A.D. McGuire, "Detection of the Free Neutrino: a Confirmation'', Science 124, 103 (1956); F. Reines and C.L. Cowan, "Detection of the Free Neutrino'', Phys. Rev. 92, 830 (1953). These papers describe the first experimental detection of neutrinos.
7. C. Darwin, On the Origin of the Species by Natural Selection, or, The Preservation of Favored Races in the Struggle for Life (London: Murray 1859), p. 285 (Pelican Preprint of first edition, 296--297, 1968).
8. R. Davis Jr., "Solar Neutrinos. II. Experimental,'' Phys. Rev. Lett. 12, 302 (1964).
9. J.N. Bahcall and R. Davis Jr., "An Account of the Development of the Solar Neutrino Problem,'' in Essays in Nuclear Astrophysics, ed. C.A. Barnes, D.D. Clayton, and D. Schramm (Cambridge: Cambridge University Press 1982), p. 243; reprinted in J.N. Bahcall, Neutrino Astrophysics, (Cambridge: Cambridge University Press 1989). For related material, see http://www.sns.ias.edu/~jnb/Papers/Popular/snhistory.html.
10. A.S. Eddington, "The Internal Constitution of the Stars,'' Observatory 43, 353 (1920). This lecture is inspiring.
11. A. Einstein, "Zur Elektrodynamik bewegter Körper,'' Annalen der Physik, 17 (105). English translation in The Principle of Relativity, translated by W. Perrett and G.B. Jeffery with notes by A. Sommerfeld, (Dover Publications: New York), 1923. The logic in this paper is breathtakingly beautiful and incredibly clear.
12. E. Fermi, "Tentativo di una teoria della emissione di raggi ,'' Ric. 4, 491 (1934). Reprinted in Enrico Fermi, Collected Papers: Note e memorie, Vol 1. p. 538 (University of Chicago Press: Chicago) (1962-1965). See also p. 559, 575. Fermi formulated the mathematical theory of neutrino emission in -decay. His first paper on the subject was rejected as "too speculative'' for publication.
13. W.A. Fowler, "Experimental and theoretical nuclear astrophysics: the quest for the origin of the elements,'' Rev. Mod. Phys. 56, 149 (1984).
14. G. Gamow, "Zur Quantentheorie der Atomzertrümmerung,'' Zeit. fur Physik 52, 510 (1928). Derives the Gamow factor using quantum mechanics.
15. S. Hawking, "Gravitationally collapsed objects of very low mass'', Monthly Notices of Royal Astronomical Society, 152, 75 (1971). In this imaginative paper, Hawking speculated that the central region of the sun might contain a black hole and that this could be the reason why the flux of solar neutrinos was less than predicted.
16. H. von Helmholtz, Lecture "On the interaction of natural forces,'' Königsberg, February 7 (1854), in Phil. Mag. 11 [series 4], 489-518 (1856).
17. J.F.W. Herschel, A Treatise on Astronomy (London 1833), p. 211.
18. W.T. Kelvin, "On the Age of the Sun's Heat,'' Macmillan's Magazine, 288--293 (March 5, 1862).
19. J. Marchant, Alfred Russel Wallace, Letters and Reminiscences, I (London: Cassell 1916), p. 242. Letter dated 14 April, 1869.
20. W. Pauli, letter to a physicists' gathering at Tübingen, December 4, 1930. Reprinted in Wolfgang Pauli, Collected Scientific Papers, ed. R. Kronig and V. Weisskopf, Vol. 2, p. 1313 (Interscience, New York) (1964).
21. H.N. Russell, "On the Sources of Stellar Energy,'' Pub. Ast. Soc. Pacific, August (1919). If you like to read mystery stories and to figure out "Who did it'' from limited clues, then you will love this paper. A year before Aston's measurements of the mass of hydrogen and of helium and two decades before Bethe's calculations of nuclear fusion rates, Russell used well-known observations of stars and simple physical reasoning to infer that the rate of the "unknown process'' that supplies stellar energy must increase rapidly with increasing stellar temperature. Incredibly, he also correctly deduced that this dependence of energy production on temperature would lead to stars being stable over very long periods of time. These insights are presented in the text of a closely-reasoned lecture that contains no equations.
22. E. Rutherford, "The Radiation and Emanation of Radium,'' Pt. II, Technics, Aug., 171, (1904) Collected Papers, I: 650.
23. C. Smith and M.N. Wise, Energy and Empire: A biographical study of Lord Kelvin, (Cambridge: Cambridge University Press), 1989. This book is a stimulating and authoritative account of Kelvin, his science, and his life. Chapters 15-17 deal with the age of the sun, the cooling of the earth, and the age of the earth.
24. C. F. von Weizsäcker, "Über Elementumwandlungen in Innern der Sterne. II,'' Physikalische Zeitschrift, 39, 633 (1938). The CNO cycle is described in the last paragraph of Section 7.
--------------------------------------------------------------------------------
1 von Helmholtz and Mayer were two of the codiscoverers of the law of conservation of energy. This law states that energy can be transformed from one form to another but the total amount is always conserved. Conservation of energy is a basic principle of modern physics that is used in analyzing the very smallest (sub-atomic) domains and the largest known structure (the universe), and just about everything in between. We shall see later that Einstein's generalization of the law of conservation of energy was a key ingredient in understanding the origin of solar radiation. The application of conservation of energy to radioactivity revealed the existence of neutrinos.
2 According to the modern theory of stellar evolution, the sun is heated to the enormous temperatures at which nuclear fusion can occur by gravitational energy released as the solar mass contracts from an initially large gas cloud. Thus, Kelvin and other nineteenth-century physicists were partially right; the release of gravitational energy ignited nuclear energy generation in the sun.
3 The sensitive dependence of the Gamow factor upon the relative energy of the two charged particles is, we now understand, what provides the temperature "thermostat'' for stars.
4 The existence of neutrinos was first proposed by Wolfgang Pauli in a 1930 letter to his physics colleagues as a "desperate way out" of the apparent non-conservation of energy in certain radioactive decays (called -decays) in which electrons were emitted. According to Pauli's hypothesis, which he put forward very hesitantly, neutrinos are elusive particles which escape with the missing energy in -decays. The mathematical theory of -decay was formulated by Enrico Fermi in 1934 in a paper which was rejected by the journal Nature because "it contained speculations too remote from reality to be of interest to the reader.'' Neutrinos from a nuclear reactor were first detected by Clyde Cowan and Fred Reines in 1956.
5 Perhaps the most imaginative proposal was made by Stephen Hawking, who suggested that the central region of the sun might contain a small black hole and that this could be the reason why the number of neutrinos observed is less than the predicted number.