Edited and Added By:
Arip Nurahman
Department of Physics
Faculty of Sciences and Mathematics, Indonesia University of Education
and Follower Open Course Ware at MIT-Harvard University, M.A., U.S.A.
A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored thermal energy. White dwarfs comprise roughly 6% of all known stars in the solar neighborhood. The unusual faintness of white dwarfs was first recognized in 1910 by Henry Norris Russell, Edward Charles Pickering, and Williamina Fleming; p. 1 the name white dwarf was coined by Willem Luyten in 1922.
(Wikipedia)
NASA's Hubble Space Telescope is providing strong evidence that white dwarfs, the burned-out relics of stars, are given a "kick" when they form.
The sharp vision of Hubble's Advanced Camera for Surveys uncovered the speedy white dwarfs in the ancient globular star cluster NGC 6397, a dense swarm of hundreds of thousands of stars.
Before the stars burned out as white dwarfs, they were among the most massive stars in NGC 6397. Because massive stars are thought to gather at a globular cluster's core, astronomers assumed that most newly minted white dwarfs dwelled near the center.
Hubble, however, discovered young white dwarfs residing at the edge of NGC 6397, which is about 11.5 billion years old.
"The distribution of young white dwarfs is the exact opposite of what we expected," said astronomer Harvey Richer of the University of British Columbia in Vancouver. "Our idea is that as aging stars evolve into white dwarfs, they are given a kick of 7,000 to 11,000 miles an hour (3 to 5 kilometers a second), which rockets them to the outer reaches of the cluster."
Richer suggested that white dwarfs propel themselves by ejecting mass, like rockets do. Before stars evolve into white dwarfs, they swell up and become red giants. Red giant stars lose about half their mass by shedding it into space. If more of this mass is ejected in one direction, it could propel the emerging white dwarf through space, just as exhaust from a rocket engine thrusts the rocket from the launch pad, Richer proposed.
Observations of some planetary nebulae display similarly directed outflows. (Planetary nebulae are the glowing material ejected by red giant stars.) The jets in those planetary nebulae are shown to flow in opposite directions. If they are not perfectly balanced, Richer reasoned, the stronger jet could accelerate the white dwarf in the opposite direction.
The idea that young white dwarfs are born with a kick was suggested 30 years ago to explain why there were so few of them in open star clusters. In 2003 Michael Fellhauer of the University of California at Santa Cruz and colleagues calculated that if white dwarfs were given a small boost, they could be expelled from open clusters. It is easier, however, for white dwarfs to escape the weak gravitational clutches of open clusters than to rocket out of globular clusters, which are as much as 100 times more massive than open clusters.
Richer and his team, therefore, decided to test the acceleration theory in a globular cluster. The astronomers chose NGC 6397 because, at 8,500 light-years away, it is one of the closest globular star clusters to Earth. About 150 globular clusters exist in the Milky Way, each containing up to a million stars.
The team studied 22 young white dwarfs less than 800 million years old and 62 older white dwarfs between 1.4 and 3.5 billion years old. The astronomers distinguished the younger from the older white dwarfs based on their color and brightness. The younger white dwarfs are hotter and therefore bluer and brighter than the older ones.
Globular clusters sort out stars according to their mass, governed by a gravitational pinball game between stars. Heavier stars slow down and sink to the cluster's core, while lighter stars pick up speed and move across the cluster to its outskirts. Richer's team found that the older white dwarfs were behaving as expected: They were scattered throughout the cluster according to weight.
The young white dwarfs, however, were found unexpectedly at the edge of the cluster, puzzling Richer and his team.
Their expected neighborhood is near the center because their progenitor stars were the heaviest stars present in the cluster. These fledgling white dwarfs are so young that they have not had enough encounters with other stars to spread them across the cluster, suggesting that some other mechanism (a kick) is at work.
"The first time we plotted up the distribution and found a difference, we thought, 'My goodness, what is happening?'" said team member Saul Davis, a graduate student at the University of British Columbia in Vancouver. "For a long time, we thought we had made a mistake. But no matter what we did, it didn't go away."
The team considered other explanations for the young white dwarfs' location. They could have been part of binary systems and gotten kicked out by their partners. Or perhaps they were given a boost after encountering heavier stars. The team, however, ruled out those explanations through computer simulations.
Richer hopes to study other globular clusters for runaway white dwarfs. The results will appear in the January 2008 issue of the Monthly Notices of Royal Astronomical Society Letters.
Other members of the team are I.R. King (University of Washington, Seattle); J. Anderson (Space Telescope Science Institute, Baltimore, Md.); J. Coffey (University of British Columbia, Vancouver); G.G. Fahlman (NRC Herzberg Institute of Astrophysics, National Research Council Canada, Saanich, British Columbia); J. Hurley (Swinburne University of Technology, Hawthorn, Australia); and J.S. Kalirai (University of California at Santa Cruz.)
Composition and structure
Although white dwarfs are known with estimated masses as low as 0.17[27] and as high as 1.33[28] solar masses, the mass distribution is strongly peaked at 0.6 solar mass, and the majority lie between 0.5 to 0.7 solar mass.[28] The estimated radii of observed white dwarfs, however, are typically between 0.008 and 0.02 times the radius of the Sun;[29] this is comparable to the Earth's radius of approximately 0.009 solar radius. A white dwarf, then, packs mass comparable to the Sun's into a volume that is typically a million times smaller than the Sun's; the average density of matter in a white dwarf must therefore be, very roughly, 1,000,000 times greater than the average density of the Sun, or approximately 106 grams (1 tonne) per cubic centimeter.[1] White dwarfs are composed of one of the densest forms of matter known, surpassed only by other compact stars such as neutron stars, black holes and, hypothetically, quark stars.[30]
White dwarfs were found to be extremely dense soon after their discovery. If a star is in a binary system, as is the case for Sirius B and 40 Eridani B, it is possible to estimate its mass from observations of the binary orbit. This was done for Sirius B by 1910,[31] yielding a mass estimate of 0.94 solar mass. (A more modern estimate is 1.00 solar mass.)[32] Since hotter bodies radiate more than colder ones, a star's surface brightness can be estimated from its effective surface temperature, and hence from its spectrum. If the star's distance is known, its overall luminosity can also be estimated. Comparison of the two figures yields the star's radius. Reasoning of this sort led to the realization, puzzling to astronomers at the time, that Sirius B and 40 Eridani B must be very dense. For example, when Ernst Öpik estimated the density of a number of visual binary stars in 1916, he found that 40 Eridani B had a density of over 25,000 times the Sun's, which was so high that he called it "impossible".[33] As Arthur Stanley Eddington put it later in 1927:[34], p. 50
We learn about the stars by receiving and interpreting the messages which their light brings to us. The message of the Companion of Sirius when it was decoded ran: "I am composed of material 3,000 times denser than anything you have ever come across; a ton of my material would be a little nugget that you could put in a matchbox." What reply can one make to such a message? The reply which most of us made in 1914 was—"Shut up. Don't talk nonsense."
As Eddington pointed out in 1924, densities of this order implied that, according to the theory of general relativity, the light from Sirius B should be gravitationally redshifted.[23] This was confirmed when Adams measured this redshift in 1925.[35]
Such densities are possible because white dwarf material is not composed of atoms bound by chemical bonds, but rather consists of a plasma of unbound nuclei and electrons. There is therefore no obstacle to placing nuclei closer to each other than electron orbitals—the regions occupied by electrons bound to an atom—would normally allow.[23] Eddington, however, wondered what would happen when this plasma cooled and the energy which kept the atoms ionized was no longer present.[36] This paradox was resolved by R. H. Fowler in 1926 by an application of the newly devised quantum mechanics. Since electrons obey the Pauli exclusion principle, no two electrons can occupy the same state, and they must obey Fermi-Dirac statistics, also introduced in 1926 to determine the statistical distribution of particles which satisfy the Pauli exclusion principle.[37] At zero temperature, therefore, electrons could not all occupy the lowest-energy, or ground, state; some of them had to occupy higher-energy states, forming a band of lowest-available energy states, the Fermi sea. This state of the electrons, called degenerate, meant that a white dwarf could cool to zero temperature and still possess high energy. Another way of deriving this result is by use of the uncertainty principle: the high density of electrons in a white dwarf means that their positions are relatively localized, creating a corresponding uncertainty in their momenta. This means that some electrons must have high momentum and hence high kinetic energy.[36][38]
Compression of a white dwarf will increase the number of electrons in a given volume. Applying either the Pauli exclusion principle or the uncertainty principle, we can see that this will increase the kinetic energy of the electrons, causing pressure.[36][39] This electron degeneracy pressure is what supports a white dwarf against gravitational collapse. It depends only on density and not on temperature. Degenerate matter is relatively compressible; this means that the density of a high-mass white dwarf is so much greater than that of a low-mass white dwarf that the radius of a white dwarf decreases as its mass increases.[1]
The existence of a limiting mass that no white dwarf can exceed is another consequence of being supported by electron degeneracy pressure. These masses were first published in 1929 by Wilhelm Anderson[40] and in 1930 by Edmund C. Stoner.[41] The modern value of the limit was first published in 1931 by Subrahmanyan Chandrasekhar in his paper "The Maximum Mass of Ideal White Dwarfs".[42] For a nonrotating white dwarf, it is equal to approximately 5.7/μe2 solar masses, where μe is the average molecular weight per electron of the star.[43], eq. (63) As the carbon-12 and oxygen-16 which predominantly compose a carbon-oxygen white dwarf both have atomic number equal to half their atomic weight, one should take μe equal to 2 for such a star,[38] leading to the commonly quoted value of 1.4 solar masses. (Near the beginning of the 20th century, there was reason to believe that stars were composed chiefly of heavy elements,[41], p. 955 so, in his 1931 paper, Chandrasekhar set the average molecular weight per electron, μe, equal to 2.5, giving a limit of 0.91 solar mass.) Together with William Alfred Fowler, Chandrasekhar received the Nobel prize for this and other work in 1983.[44] The limiting mass is now called the Chandrasekhar limit.
If a white dwarf were to exceed the Chandrasekhar limit, and nuclear reactions did not take place, the pressure exerted by electrons would no longer be able to balance the force of gravity, and it would collapse into a denser object such as a neutron star.[45] However, carbon-oxygen white dwarfs accreting mass from a neighboring star undergo a runaway nuclear fusion reaction, which leads to a Type Ia supernova explosion in which the white dwarf is destroyed, just before reaching the limiting mass.[46]
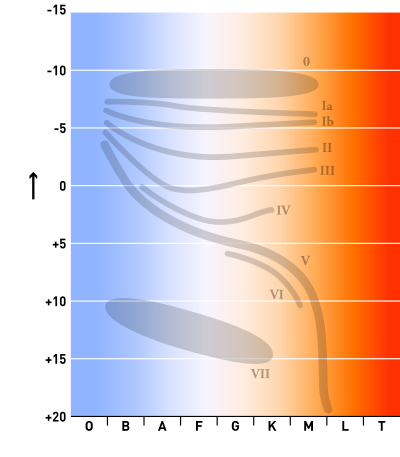
White dwarfs have low luminosity and therefore occupy a strip at the bottom of the Hertzsprung-Russell diagram, a graph of stellar luminosity versus color (or temperature). They should not be confused with low-luminosity objects at the low-mass end of the main sequence, such as the hydrogen-fusing red dwarfs, whose cores are supported in part by thermal pressure,[47] or the even lower-temperature brown dwarfs.[48]
Mass-radius relationship and mass limit
It is simple to derive a rough relationship between the mass and radii of white dwarfs using an energy minimization argument. The energy of the white dwarf can be approximated by taking it to be the sum of its gravitational potential energy and kinetic energy. The gravitational potential energy of a unit mass piece of white dwarf, Eg, will be on the order of −GM/R, where G is the gravitational constant, M is the mass of the white dwarf, and R is its radius. The kinetic energy of the unit mass, Ek, will primarily come from the motion of electrons, so it will be approximately N p2/2m, where p is the average electron momentum, m is the electron mass, and N is the number of electrons per unit mass. Since the electrons are degenerate, we can estimate p to be on the order of the uncertainty in momentum, Δp, given by the uncertainty principle, which says that Δp Δx is on the order of the reduced Planck constant, ħ. Δx will be on the order of the average distance between electrons, which will be approximately n−1/3, i.e., the reciprocal of the cube root of the number density, n, of electrons per unit volume. Since there are N M electrons in the white dwarf and its volume is on the order of R3, n will be on the order of N M / R3.[38]
Solving for the kinetic energy per unit mass, Ek, we find that
The white dwarf will be at equilibrium when its total energy, Eg + Ek, is minimized. At this point, the kinetic and gravitational potential energies should be comparable, so we may derive a rough mass-radius relationship by equating their magnitudes:
Solving this for the radius, R, gives[38]
Dropping N, which depends only on the composition of the white dwarf, and the universal constants leaves us with a relationship between mass and radius:
i.e., the radius of a white dwarf is inversely proportional to the cube root of its mass.
Since this analysis uses the non-relativistic formula p2/2m for the kinetic energy, it is non-relativistic. If we wish to analyze the situation where the electron velocity in a white dwarf is close to the speed of light, c, we should replace p2/2m by the extreme relativistic approximation p c for the kinetic energy. With this substitution, we find
If we equate this to the magnitude of Eg, we find that R drops out and the mass, M, is forced to be[38]
To interpret this result, observe that as we add mass to a white dwarf, its radius will decrease, so, by the uncertainty principle, the momentum, and hence the velocity, of its electrons will increase. As this velocity approaches c, the extreme relativistic analysis becomes more exact, meaning that the mass M of the white dwarf must approach Mlimit. Therefore, no white dwarf can be heavier than the limiting mass Mlimit.
For a more accurate computation of the mass-radius relationship and limiting mass of a white dwarf, one must compute the equation of state which describes the relationship between density and pressure in the white dwarf material. If the density and pressure are both set equal to functions of the radius from the center of the star, the system of equations consisting of the hydrostatic equation together with the equation of state can then be solved to find the structure of the white dwarf at equilibrium. In the non-relativistic case, we will still find that the radius is inversely proportional to the cube root of the mass.[43], eq. (80) Relativistic corrections will alter the result so that the radius becomes zero at a finite value of the mass. This is the limiting value of the mass—called the Chandrasekhar limit—at which the white dwarf can no longer be supported by electron degeneracy pressure. The graph on the right shows the result of such a computation. It shows how radius varies with mass for non-relativistic (blue curve) and relativistic (green curve) models of a white dwarf. Both models treat the white dwarf as a cold Fermi gas in hydrostatic equilibrium. The average molecular weight per electron, μe, has been set equal to 2. Radius is measured in standard solar radii and mass in standard solar masses.[43][49]
These computations all assume that the white dwarf is nonrotating. If the white dwarf is rotating, the equation of hydrostatic equilibrium must be modified to take into account the centrifugal pseudo-force arising from working in a rotating frame.[50] For a uniformly rotating white dwarf, the limiting mass increases only slightly. However, if the star is allowed to rotate nonuniformly, and viscosity is neglected, then, as was pointed out by Fred Hoyle in 1947,[51] there is no limit to the mass for which it is possible for a model white dwarf to be in static equilibrium. Not all of these model stars, however, will be dynamically stable.[52]
References
- ^ a b c d e f g h Extreme Stars: White Dwarfs & Neutron Stars, Jennifer Johnson, lecture notes, Astronomy 162, Ohio State University. Accessed on line May 3, 2007.
- ^ The One Hundred Nearest Star Systems, Todd J. Henry, RECONS, April 11, 2007. Accessed on line May 4, 2007.
- ^ a b c d White Dwarfs, E. Schatzman, Amsterdam: North-Holland, 1958.
- ^ a b c d How Degenerate Stars Came to be Known as White Dwarfs, J. B. Holberg, Bulletin of the American Astronomical Society 37 (December 2005), p. 1503.
- ^ a b c d The Potential of White Dwarf Cosmochronology, G. Fontaine, P. Brassard, and P. Bergeron, Publications of the Astronomical Society of the Pacific 113, #782 (April 2001), pp. 409–435.
- ^ a b c d e Late stages of evolution for low-mass stars, Michael Richmond, lecture notes, Physics 230, Rochester Institute of Technology. Accessed on line May 3, 2007.
- ^ a b On Possible Oxygen/Neon White Dwarfs: H1504+65 and the White Dwarf Donors in Ultracompact X-ray Binaries, K. Werner, N. J. Hammer, T. Nagel, T. Rauch, and S. Dreizler, pp. 165 ff. in 14th European Workshop on White Dwarfs; Proceedings of a meeting held at Kiel, July 19–23, 2004, edited by D. Koester and S. Moehler, San Francisco: Astronomical Society of the Pacific, 2005.
- ^ a b A Helium White Dwarf of Extremely Low Mass, James Liebert, P. Bergeron, Daniel Eisenstein, H.C. Harris, S.J. Kleinman, Atsuko Nitta, and Jurek Krzesinski, The Astrophysical Journal 606, #2 (May 2004), pp. L147–L149. Accessed on line March 5, 2007.
Perbaikan:
Ke-1: 11-10-2009
Arip Nurahman
(Teacher and Professional Lecturer)
Guru dan Dosen Profesional
(Teacher and Professional Lecturer)
Guru dan Dosen Profesional
Semoga Bermanfaat dan Terima Kasih





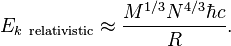


























No comments:
Post a Comment