Indonesian Space Sciences & Technology School
A rocket or rocket vehicle is a missile, spacecraft, aircraft or other vehicle which obtains thrust from a rocket engine. In all rockets, the exhaust is formed entirely from propellants carried within the rocket before use.[1] Rocket engines work by action and reaction. Rocket engines push rockets forwards simply by throwing their exhaust backwards extremely fast.
Rockets, in military and recreational uses, date back to at least the 13th century.[2] Significant scientific, interplanetary and industrial use did not occur until the 20th century, when rocketry was the enabling technology of the Space Age, including setting foot on the moon.
Rockets are used for fireworks, weaponry, ejection seats, launch vehicles for artificial satellites, human spaceflight and exploration of other planets. While comparatively inefficient for low speed use, they are very lightweight and powerful, capable of generating large accelerations and of attaining extremely high speeds with reasonable efficiency.
Chemical rockets are the most common type of rocket and they typically create their exhaust by the combustion of rocket propellant. Chemical rockets store a large amount of energy in an easily released form, and can be very dangerous. However, careful design, testing, construction and use minimizes risks.
Physics
Operation
Main article: Rocket engine
The action of the rocket engine's combustion chambers and expansion nozzles on a high pressure fluid is able to accelerate the fluid to extremely high speed, and conversely this exerts a large reactive thrust on the rocket (an equal and opposite reaction according to Newton's third law) which propels the rocket forwards.In a closed chamber, the pressures are equal in each direction and no acceleration occurs. If an opening is provided in the bottom of the chamber then the pressure is no longer acting on the missing section. This opening permits the exhaust to escape. The remaining pressures give a resultant thrust on the side opposite the opening, and these pressures are what push the rocket along.
Using a nozzle gives more force as well since the exhaust also presses on it as it expands outwards, roughly doubling the total force. If propellant gas is continuously added to the chamber then these pressures can be maintained for as long as propellant remains.[1]
As a side effect, these pressures on the rocket also act on the exhaust in the opposite direction and accelerate this to very high speeds (according to Newton's Third Law).[1] From the principle of conservation of momentum the speed of the exhaust of a rocket determines how much momentum increase is created for a given amount of propellant. This is called the rocket's specific impulse.[1] Because a rocket, propellant and exhaust in flight, without any external perturbations, may be considered as a closed system, the total momentum is always constant. Therefore, the faster the net speed of the exhaust in one direction, the greater the speed of the rocket can achieve in the opposite direction. This is especially true since the rocket body's mass is typically far lower than the final total exhaust mass.
As the remaining propellant decreases, rocket vehicles become lighter and their acceleration tends to increase until the propellant is exhausted. This means that much of the speed change occurs towards the end of the burn when the vehicle is much lighter.[1]
Forces on a rocket in flight

Forces on a rocket in flight, rockets that must travel through the air are usually tall and thin as this shape gives a high ballistic coefficient and minimizes drag losses
The general study of the forces on a rocket or other spacecraft is part of ballistics and is called astrodynamics.
Flying rockets are primarily affected by the following:[76]
- Thrust from the engine(s)
- Gravity from celestial bodies
- Drag if moving in atmosphere
- Lift; usually relatively small effect except for rocket-powered aircraft
In addition, the inertia and centrifugal pseudo-force can be significant due to the path of the rocket around the center of a celestial body; when high enough speeds in the right direction and altitude are achieved a stable orbit or escape velocity is obtained.
These forces, with a stabilizing tail (the empennage) present will, unless deliberate control efforts are made, naturally cause the vehicle to follow a roughly parabolic trajectory termed a gravity turn, and this trajectory is often used at least during the initial part of a launch. (This is true even if the rocket engine is mounted at the nose.) Vehicles can thus maintain low or even zero angle of attack which minimizes transverse stress on the launch vehicle; permitting a weaker, and hence lighter, launch vehicle.[77][78]
Net thrust

Due to the supersonic nature of the exhaust jet the exit pressure can be different to ambient atmospheric pressure. Nozzles are said to be (top to bottom):
• Underexpanded (above ambient).
• Ambient.
• Overexpanded (below ambient).
• Grossly overexpanded.
If under or overexpanded then loss of efficiency occurs, grossly overexpanded nozzles lose less efficiency, but the exhaust jet is usually unstable. Rockets become progressively more underexpanded as they gain altitude. Note that almost all rocket engines will be momentarily grossly overexpanded during startup in an atmosphere.[79]
• Underexpanded (above ambient).
• Ambient.
• Overexpanded (below ambient).
• Grossly overexpanded.
If under or overexpanded then loss of efficiency occurs, grossly overexpanded nozzles lose less efficiency, but the exhaust jet is usually unstable. Rockets become progressively more underexpanded as they gain altitude. Note that almost all rocket engines will be momentarily grossly overexpanded during startup in an atmosphere.[79]
For a more detailed model of the net thrust of a rocket engine that includes the effect of atmospheric pressure, see Rocket_engine#Net_thrust.
A typical rocket engine can handle a significant fraction of its own mass in propellant each second, with the propellant leaving the nozzle at several kilometres per second. This means that the thrust-to-weight ratio of a rocket engine, and often the entire vehicle can be very high, in extreme cases over 100. This compares with other jet propulsion engines that can exceed 5 for some of the better[80] engines.[81]
The propellant flow rate of a rocket is often deliberately varied over a flight, to provide a way to control the thrust and thus the airspeed of the vehicle. This, for example, allows minimization of aerodynamic losses[82] and can limit the increase of g-forces due to the reduction in propellant load.
It can be shown that the net thrust of a rocket is:
where:
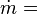 propellant flow (kg/s or lb/s)
propellant flow (kg/s or lb/s)
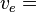 the effective exhaust velocity (m/s or ft/s)
the effective exhaust velocity (m/s or ft/s)
The effective exhaust velocity ve is more or less the speed the exhaust leaves the vehicle, and in the vacuum of space, the effective exhaust velocity is often equal to the actual average exhaust speed along the thrust axis. However, the effective exhaust velocity allows for various losses, and notably, is reduced when operated within an atmosphere.
Impulse
Main article: Impulse
The total impulse of a rocket burning its propellant is simply:[84]Specific impulse
Main article: specific impulse
As can be seen from the thrust equation the effective speed of the exhaust controls the amount of thrust produced from a particular quantity of fuel burnt per second.
An equivalent measure, the net thrust-seconds (impulse) per weight unit of propellant expelled is called specific Impulse "Isp" and this is one of the most important figures that describes a rocket's performance. It is defined such that it is related to the effective exhaust velocity by:
where:
- Isp has units of seconds
- g0 is the acceleration at the surface of the Earth
Thus, the greater the specific impulse, the greater the net thrust and performance of the engine. Isp is determined by measurement while testing the engine. In practice the effective exhaust velocities of rockets varies but can be extremely high, ~4500 m/s, about 15 times the sea level speed of sound in air.
- Typical performances of common propellants
| Propellant mix | Vacuum Isp (seconds) | Effective exhaust velocity (m/s) |
|---|---|---|
| liquid oxygen/ liquid hydrogen | 455 | 4462 |
| liquid oxygen/ kerosene (RP-1) | 358 | 3510 |
| nitrogen tetroxide/ hydrazine | 305 | 2993 |
n.b. All performances at a nozzle expansion ratio of 40
Delta-v (rocket equation)
Main article: Tsiolkovsky rocket equation
The delta-v capacity of a rocket is the theoretical total change in velocity that a rocket can achieve without any external interference (without air drag or gravity or other forces).When ve is constant, the delta-v that a rocket vehicle can provide can be calculated from the Tsiolkovsky rocket equation:[88]
- m0 is the initial total mass, including propellant, in kg (or lb)
- m1 is the final total mass in kg (or lb)
- ve is the effective exhaust velocity in m/s or (ft/s)
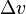 is the delta-v in m/s (or ft/s)
is the delta-v in m/s (or ft/s)
When launched from the Earth practical delta-v's for a single rockets carrying payloads can be a few km/s. Some theoretical designs have rockets with delta-v's over 9 km/s.
The required delta-v can also be calculated for a particular manoeuvre; for example the delta-v to launch from the surface of the Earth to Low earth orbit is about 9.7 km/s, which leaves the vehicle with a sideways speed of about 7.8 km/s at an altitude of around 200 km. In this manoeuvre about 1.9 km/s is lost in air drag, gravity drag and gaining altitude.
The ratio
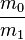 is sometimes called the mass ratio.
is sometimes called the mass ratio.Mass ratios
Main article: mass ratio
Persons not familiar with spaceflight rarely realize that almost all of a launch vehicle's mass consists of propellant.[89] Mass ratio is, for any 'burn', the ratio between the rocket's initial mass and the mass after.[90] Everything else being equal, a high mass ratio is desirable for good performance, since it indicates that the rocket is lightweight and hence performs better, for essentially the same reasons that low weight is desirable in sports cars.
Rockets as a group have the highest thrust-to-weight ratio of any type of engine; and this helps vehicles achieve high mass ratios, which improves the performance of flights. The higher the ratio, the less engine mass is needed to be carried. This permits the carrying of even more propellant, enormously improving the delta-v. Alternatively, some rockets such as for rescue scenarios or racing carry relatively little propellant and payload and thus need only a lightweight structure and instead achieve high accelerations. For example, the Soyuz escape system can produce 20g.[71]
Achievable mass ratios are highly dependent on many factors such as propellant type, the design of engine the vehicle uses, structural safety margins and construction techniques.
The highest mass ratios are generally achieved with liquid rockets, and these types are usually used for orbital launch vehicles, a situation which calls for a high delta-v. Liquid propellants generally have densities similar to water (with the notable exceptions of liquid hydrogen and liquid methane), and these types are able to use lightweight, low pressure tanks and typically run high-performance turbopumps to force the propellant into the combustion chamber.
Some notable mass fractions are found in the following table (some aircraft are included for comparison purposes):
| Vehicle | Takeoff Mass | Final Mass | Mass ratio | Payload fraction |
|---|---|---|---|---|
| Ariane 5 (vehicle + payload) | 746,000 kg [91] (~1,645,000 lb) | 2,700 kg + 16,000 kg[91] (~6,000 lb + ~35,300 lb) | 39.9 | 0.975 |
| Titan 23G first stage | 117,020 kg (258,000 lb) | 4,760 kg (10,500 lb) | 24.6 | 0.959 |
| Saturn V | 3,038,500 kg[92] (~6,700,000 lb) | 13,300 kg + 118,000 kg[92] (~29,320 lb + ~260,150 lb) | 23.1 | 0.957 |
| Space Shuttle (vehicle + payload) | 2,040,000 kg (~4,500,000 lb) | 104,000 kg + 28,800 kg (~230,000 lb + ~63,500 lb) | 15.4 | 0.935 |
| Saturn 1B (stage only) | 448,648 kg[93] (989,100 lb) | 41,594 kg[93] (91,700 lb) | 10.7 | 0.907 |
| Virgin Atlantic GlobalFlyer | 10,024.39 kg (22,100 lb) | 1,678.3 kg (3,700 lb) | 6.0 | 0.83 |
| V2 | 13,000 kg (~28,660 lb) (12.8 ton) | 3.85 | 0.74 [94] | |
| X-15 | 15,420 kg (34,000 lb) | 6,620 kg (14,600 lb) | 2.3 | 0.57[95] |
| Concorde | ~181,000 kg (400,000 lb [95]) | 2 | 0.5[95] | |
| Boeing 747 | ~363,000 kg (800,000 lb[95]) | 2 | 0.5[95] |
Staging
Main article: Multistage rocket
Often, the required velocity (delta-v) for a mission is unattainable by any single rocket because the propellant, tankage, structure, guidance, valves and engines and so on, take a particular minimum percentage of take-off mass that is too great for the propellant it carries to achieve that delta-v.
For example the first stage of the Saturn V, carrying the weight of the upper stages, was able to achieve a mass ratio of about 10, and achieved a specific impulse of 263 seconds. This gives a delta-v of around 5.9 km/s whereas around 9.4 km/s delta-v is needed to achieve orbit with all losses allowed for.
This problem is frequently solved by staging — the rocket sheds excess weight (usually empty tankage and associated engines) during launch. Staging is either serial where the rockets light after the previous stage has fallen away, or parallel, where rockets are burning together and then detach when they burn out.[96]
The maximum speeds that can be achieved with staging is theoretically limited only by the speed of light. However the payload that can be carried goes down geometrically with each extra stage needed, while the additional delta-v for each stage is simply additive.
Acceleration and thrust-to-weight ratio
Main article: thrust-to-weight ratio
From Newton's second law the acceleration of a vehicle is simply:Where m is the instantaneous mass of the vehicle and Fn is the net force acting on the rocket (mostly thrust but air drag and other forces can play a part.)
Typically, the acceleration of a rocket increases with time (if the thrust stays the same) as the weight of the rocket decreases as propellant is burned, but the thrust can be throttled to offset or vary this if needed. Discontinuities in acceleration will also occur when stages burn out, often starting at a lower acceleration with each new stage firing.
Peak accelerations can be increased by designing the vehicle with a reduced mass, usually achieved by a reduction in the fuel load and tankage and associated structures, but obviously this reduces range, delta-v and burn time. Still, for some applications that rockets are used for, a high peak acceleration applied for just a short time is highly desirable.
The minimal mass of vehicle consists of a rocket engine with minimal fuel and structure to carry it. In that case the thrust-to-weight ratio[nb 4] of the rocket engine limits the maximum acceleration that can be designed. It turns out that rocket engines generally have truly excellent thrust to weight ratios (137 for the NK-33 engine,[98] some solid rockets are over 1000[97]), and nearly all really high-g vehicles employ or have employed rockets.
The high accelerations that rockets naturally possess means that rocket vehicles are often capable of vertical takeoff; this can be done provided the vehicles engines provide more than the local gravitational acceleration away from the Earth or gravity source.
Drag
Drag is a force which acts opposite to the direction of the rocket's motion. This will cause a decrease in the acceleration of the vehicle whilst also producing structural loads. The deceleration force for fast-moving rockets can be calculated using the drag equation.
Drag can be minimised by an aerodynamic nose cone and by using a shape with a high ballistic coefficient (the "classic" rocket shape - long and thin).
During a rocket launch, as the vehicle speed increases, and the atmosphere thins, there is a point of maximum aerodynamic drag called Max Q. This determines the minimum aerodynamic strength of the vehicle, as the rocket must avoid buckling under these forces.[82]
Energy
Energy efficiency
Main article: propulsive efficiency
Rocket launch vehicles take-off with a great deal of flames, noise and drama, and it might seem obvious that they are grievously inefficient. However, while they are far from perfect, their energy efficiency is not as bad as might be supposed.
The energy density of a typical rocket propellant is often around one-third that of conventional hydrocarbon fuels; the bulk of the mass is (often relatively inexpensive) oxidizer. Nevertheless, at take-off the rocket has a great deal of energy in the fuel and oxidizer stored within the vehicle. It is of course desirable that as much of the energy of the propellant end up as kinetic or potential energy of the body of the rocket as possible.
Energy from the fuel is lost in air drag and gravity drag and is used for the rocket to gain altitude and speed. However, much of the lost energy ends up in the exhaust.[99]
100% efficiency within the engine (engine efficiency ηc = 100%) would mean that all the heat energy of the combustion products is converted into kinetic energy of the jet. This is not possible, but the high expansion ratio nozzles that can be used with rockets come surprisingly close: when the nozzle expands the gas, the gas is cooled and accelerated, and an energy efficiency of up to 70% can be achieved. Most of the rest is heat energy in the exhaust that is not recovered.[99] The high efficiency is a consequence of the fact that rocket combustion can be performed at very high temperatures and the gas is finally released at much lower temperatures, and so giving good Carnot efficiency.
However, engine efficiency is not the whole story. In common with the other jet-based engines, but particularly in rockets due to their high and typically fixed exhaust speeds, rocket vehicles are extremely inefficient at low speeds irrespective of the engine efficiency. The problem is that at low speeds, the exhaust carries away a huge amount of kinetic energy rearward. This phenomenon is termed propulsive efficiency (ηp).[99]
However, as speeds rise, the resultant exhaust speed goes down, and the overall vehicle energetic efficiency rises, reaching a peak of around 100% of the engine efficiency when the vehicle is travelling exactly at the same speed that the exhaust is emitted. In this case the exhaust would ideally stop dead in space behind the moving vehicle, taking away zero energy, and from conservation of energy, all the energy would end up in the vehicle. The efficiency then drops off again at even higher speeds as the exhaust ends up travelling forwards- trailing behind the vehicle.
Rocket propulsive efficiency as a function of vehicle speed divided by effective exhaust speed
And the overall energy efficiency η is:
- η = ηpηc
For example, from the equation, with an ηc of 0.7, a rocket flying at Mach 0.85 (which most aircraft cruise at) with an exhaust velocity of Mach 10, would have a predicted overall energy efficiency of 5.9%, whereas a conventional, modern, air breathing jet engine achieves closer to 35% efficiency. Thus a rocket would need about 6x more energy; and allowing for the specific energy of rocket propellant being around one third that of conventional air fuel, roughly 18x more mass of propellant would need to be carried for the same journey. This is why rockets are rarely if ever used for general aviation.
Since the energy ultimately comes from fuel, these considerations mean that rockets are mainly useful when a very high speed is required, such as ICBMs or orbital launch. For example NASA's space shuttle fires its engines for around 8.5 minutes, consuming 1,000 tonnes of solid propellant (containing 16% aluminium) and an additional 2,000,000 litres of liquid propellant (106,261 kg of liquid hydrogen fuel) to lift the 100,000 kg vehicle (including the 25,000 kg payload) to an altitude of 111 km and an orbital velocity of 30,000 km/h. At this altitude and velocity, the vehicle has a kinetic energy of about 3 TJ and a potential energy of roughly 200 GJ. Given the initial energy of 20 TJ,[nb 5] the Space Shuttle is about 16% energy efficient at launching the orbiter.
Thus jet engines which have a better match between speed and jet exhaust speed such as turbofans (in spite of their worse ηc) dominate for subsonic and supersonic atmospheric use while rockets work best at hypersonic speeds. On the other hand rockets do also see many short-range relatively low speed military applications where their low-speed inefficiency is outweighed by their extremely high thrust and hence high accelerations.
Oberth effect
Main article: Oberth effect
One subtle feature of rockets relates to energy. A rocket stage, while carrying a given load, is capable of giving a particular delta-v. This delta-v means that the speed will increase (or decrease) by a particular amount, which is independent of the initial speed. However, because kinetic energy is a square law on speed, this means that the faster the rocket is travelling before the burn the more energy it gains or loses.
This fact is used in interplanetary travel. It means that the amount of delta-v to reach other planets, over and above that to reach escape velocity can be much less if the delta-v is applied when the rocket is travelling at high speeds, close to the Earth or other planetary surface; whereas waiting till the rocket has slowed at altitude multiplies up the effort required to achieve the desired trajectory.
References
- Allen, H. Julian; Eggers, A. J. (1958), A Study of the Motion and Aerodynamic Heating of Ballistic Missiles Entering the Earth's Atmosphere at High Supersonic Speeds, NACA, OCLC 86134556, http://naca.central.cranfield.ac.uk/reports/1958/naca-report-1381.pdf
- Baker, A. D. (2000), Combat Fleets of the World 2000-2001, Annapolis: US Naval Institute Press, ISBN 9781557501974
- Béon, Yves (1997), Planet Dora: A Memoir of the Holocaust and the Birth of the Space Age, translated from the French La planète Dora by Béon & Richard L. Fague, Westview Press, Div. of Harper Collins, ISBN 0-8133-3272-9
- Buchanan, Brenda (2006), Gunpowder, Explosives and the State, Aldershot: Ashgate, ISBN 9780754652595
- Governing agencies
- about the rocket in israel
- FAA Office of Commercial Space Transportation
- National Aeronautics and Space Administration (NASA)
- National Association of Rocketry (USA)
- Tripoli Rocketry Association
- Asoc. Coheteria Experimental y Modelista de Argentina
- United Kingdom Rocketry Association
- IMR - German/Austrian/Swiss Rocketry Association
- Canadian Association of Rocketry
- Indian Space Research Organisation
- Information sites
Wikipedia




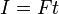

































No comments:
Post a Comment