Memahami Persamaan Navier-Stokes

Bagaimana Persamaan Navier-Stokes dapat mensimulasikan sistem udara di suatu daerah?

Atau bisakah persamaan ini memodelkan suatu badai seperti Tornado dan El-Nino?

Persamaan Navier-stokes (PNS) adalah sistem persamaan differensial non-linier yang mendeskripsikan bagaimana fluida mengalir. 

Apa itu fluida? 

Fluida adalah subtansi yang bisa mengalir seperti gas atau air.  

PNS bisa menjawab pertanyaan-pertanyaan keren tetang kehidupan sehari-hari seperti bagaimana pesawat bisa terbang?

Atau Berapa waktu yang dibutuhkan secangkir kopi yang diaduk untuk menjadi tenang?

Intro:

In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the stress in the fluid is the sum of a diffusing viscous term (proportional to the gradient of velocity) and a pressure term - hence describing viscous flow.

The equations are useful because they describe the physics of many things of academic and economic interest. They may be used to model the weather, ocean currents, water flow in a pipe and air flow around a wing. The Navier–Stokes equations in their full and simplified forms help with the design of aircraft and cars, the study of blood flow, the design of power stations, the analysis of pollution, and many other things. Coupled with Maxwell's equations they can be used to model and study magnetohydrodynamics.

The Navier–Stokes equations are also of great interest in a purely mathematical sense. Somewhat surprisingly, given their wide range of practical uses, mathematicians have not yet proven that, in three dimensions, solutions always exist (existence), or that if they do exist, then they do not contain any singularity (smoothness). These are called the Navier–Stokes existence and smoothness problems.

The Clay Mathematics Institute has called this one of the seven most important open problems in mathematics and has offered a US$1,000,000 prize for a solution or a counter-example.

Penurunan Persamaan Navier-Stokes

The derivation of the Navier–Stokes equations begins with an application of Newton's second law: conservation of momentum (often alongside mass and energy conservation) being written for an arbitrary portion of the fluid. In an inertial frame of reference, the general form of the equations of fluid motion is:

Navier–Stokes equations (general)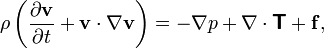

where v is the flow velocity, ρ is the fluid density, p is the pressure, 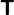is the (deviatoric) component of the total stress tensor, and f represents body forces (per unit volume) acting on the fluid and ∇ is the del operator. This is a statement of the conservation of momentum in a fluid and it is an application of Newton's second law to a continuum; in fact this equation is applicable to any non-relativistic continuum and is known as the Cauchy momentum equation.


This equation is often written using the material derivative Dv/Dt, making it more apparent that this is a statement of Newton's second law:

The left side of the equation describes acceleration, and may be composed of time dependent or convective effects (also the effects of non-inertial coordinates if present). The right side of the equation is in effect a summation of body forces (such as gravity) and divergence of stress (pressure and shear stress).

Jean Leonard Marie Poiseuille dan Gotthilf Heinrich Ludwig Hagen adalah orang yang pertama menulis tentang aliran fuida. Mereka membahas mengenai masalah aliran darah di dalam pembuluh darah. Mereka menulis tanpa melibatkan pengaruh viskositas. 

Claude Louis Marie Navier dan Sir George Gabriel Stokes merumuskan persamaan yang melibatkan viskositas dan persamaan tersebut dinamakan persamaan Navier-Stokes. Persamaan ini sangat sulit sehingga hanya bisa menjelaskan fenomene yang sederhana, contohnya adalah laminar. 

Persamaan Bernoulli berhasil diturunkan dari persamaan ini. Persamaan Bernoulli berlaku untuk fuida yang memiliki kecepatan relatif rendah. Garis arus fuida belum pecah pada kecepatan ini. Apabila kecepatan fuida ditambah maka garis arus fuida akan pecah dan berolak. 

Pecahnya garis arus dan timbulnya arus eddi dikenal sebagai fenomena turbulensi. Kapan terjadinya arus laminar dan turbulensi belum bisa terpecahkan sampai Osborne Reynolds memperkenalkan bilangan reynolds. 

Bilangan Reynold ini berbanding lurus dengan kecepatan, massa jenis fuida dan diameter pipa yang dilalui fuida serta berbanding terbalik dengan viskositas.

"Kemajuan dan Kesempurnaan Sains, Fisika dan Matematika memiliki hubungan yang erat dengan Kesejahteraan dan Kemajuan Suatu Bangsa"

*Arip Nurahman*

Sources: 

Arip Nurahman Notes

Jani Suhamjani, S.Si.

Wikipedia

NASA Glenn Research Center

Semoga Bermanfaat